题目内容
1．方程|2x-3y+1|+（3x-y+m）2=0的解满足x＜y，求m的取值范围？分析 根据非负数的性质得出x、y，由x＜y得到关于m的不等式，解之可得．
解答 解：∵|2x-3y+1|+（3x-y+m）2=0，
∴$\left\{\begin{array}{l}{2x-3y=-1}\\{3x-y=-m}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=\frac{-3m+1}{7}}\\{y=\frac{-2m+3}{7}}\end{array}\right.$，
∵x＜y，
∴$\frac{-3m+1}{7}$＜$\frac{-2m+3}{7}$，
解得：m＞-2．
点评 本题主要考查解二元一次方程组和一元一次不等式的能力，根据非负数的性质得出关于x、y的方程组和关于m的不等式是解题的关键．
练习册系列答案
相关题目
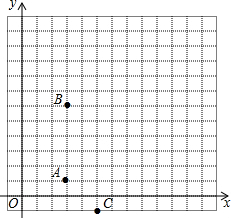某城市的街道恰好呈东西与南北横纵交错格局（如图所示），一次，警察局电子监控器屏幕上发现一辆作案后的小轿车正在点A（3，1）处以每分钟0.5个单位长度的速度向北逃窜，根据各街道的交通状况进行分析，逃犯很可能逃到点B（3，6）后改为向东逃窜，此时正在点C（5，-1）处巡逻的警车接到指令后立即以每分钟0.7个单位长度的速度进行追捕，逃犯将在什么地方被追捕到？
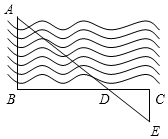为了估计河的宽度，我们可以在河对岸的岸边选定一个目标记为点A，再在河的这一边选点B和点C，使得AB⊥BC，设BC与AE交于点D，如图所示测得BD=120m，DC=40m，EC=30m，那么这条河的大致宽度是（ ）