题目内容
已知△ABC中,∠A是锐角,AB=AC,AC、AB边上的高分别为BE、CF,求证:BE=CF,画出图形并证明.
考点:等腰三角形的性质
专题:证明题
分析:根据AAS即可证明△ABE≌△ACF,根据全等三角形的对应边相等就可以证明BE=CF.
解答:证明:∵BE⊥AC于点E,CF⊥AB于点F,
∴∠AEB=∠AFC=90°,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS).
∴BE=CF.

∴∠AEB=∠AFC=90°,
在△ABE和△ACF中,
|
∴△ABE≌△ACF(AAS).
∴BE=CF.
点评:本题考查了直角三角形全等的判定及性质;此题比较简单,利用全等三角形的判定及性质就可以解题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
两个五次多项式相加,所得结果的次数是( )
| A、5 | B、10 |
| C、不大于5 | D、不小于5 |
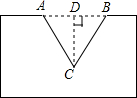 如图,工件上有一V型陶(AC=BC),测得它的上口宽20毫米,深19.2毫米,求V型角∠ACB的度数.
如图,工件上有一V型陶(AC=BC),测得它的上口宽20毫米,深19.2毫米,求V型角∠ACB的度数. 如图,△ABC内接于⊙O,且AB=BC=AC,M是
如图,△ABC内接于⊙O,且AB=BC=AC,M是
 如图,在?ABCD中,点E、F在对角线BD上,DE=BF.
如图,在?ABCD中,点E、F在对角线BD上,DE=BF.