题目内容
5.若$\sqrt{(m-2)^{2}}$+|m-3|化简的结果为一个常数,则m的取值范围是( )| A. | m>0 | B. | m≥3 | C. | m≤2 | D. | 2≤m≤3 |
分析 根据$\sqrt{(m-2)^{2}}$+|m-3|化简的结果为一个常数,可得:$\left\{\begin{array}{l}{m-2≥0}\\{m-3≤0}\end{array}\right.$,据此求出m的取值范围即可.
解答 解:$\sqrt{(m-2)^{2}}$+|m-3|=|m-2|+|m-3|
∵$\sqrt{(m-2)^{2}}$+|m-3|化简的结果为一个常数,
∴$\left\{\begin{array}{l}{m-2≥0}\\{m-3≤0}\end{array}\right.$,
解得2≤m≤3.
故选:D.
点评 此题主要考查了二次根式的性质与化简,以及绝对值的含义和求法,要熟练掌握.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.正比例函数y=3x的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
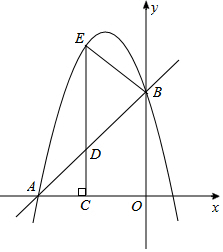 如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.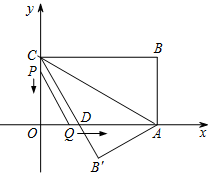 如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(6,0),将△ABC沿AC翻折,使点B落到点B′处,B′C交x轴于点D,且CD=2DB′.动点P从点C出发,沿CO以每秒1个单位的速度向点O运动;动点Q从点O出发,沿OA、AB以每秒3个单位的速度向点B运动,连接PQ.若P、Q两点同时出发,当其中一点到达终时整个运动随之结束,设运动时间为t秒.
如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(6,0),将△ABC沿AC翻折,使点B落到点B′处,B′C交x轴于点D,且CD=2DB′.动点P从点C出发,沿CO以每秒1个单位的速度向点O运动;动点Q从点O出发,沿OA、AB以每秒3个单位的速度向点B运动,连接PQ.若P、Q两点同时出发,当其中一点到达终时整个运动随之结束,设运动时间为t秒.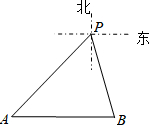 如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).
如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).