题目内容
17. 如图AE是∠BAC的平分线,BD是中线,AE、BD相交于点E,EF⊥AB于F,若AB=14,AC=12,S△BDC=20,则EF的长为2.
如图AE是∠BAC的平分线,BD是中线,AE、BD相交于点E,EF⊥AB于F,若AB=14,AC=12,S△BDC=20,则EF的长为2.
分析 先过点E作EG⊥AC,设EF=EG=x,根据△ABD的面积=20,得出△ABE的面积+△ADE的面积=20,即$\frac{1}{2}$×14×x+$\frac{1}{2}$×6×x=20,求得x的值即可.
解答  解:过点E作EG⊥AC,
解:过点E作EG⊥AC,
∵AE是∠BAC的平分线,EF⊥AB于F,
∴EF=EG,
设EF=EG=x,
∵BD是中线,S△BDC=20,AD=$\frac{1}{2}$AC=6,
∴△ABD的面积=20,
即△ABE的面积+△ADE的面积=20,
∴$\frac{1}{2}$×AB×EF+$\frac{1}{2}$×AD×EG=20,
∴$\frac{1}{2}$×14×x+$\frac{1}{2}$×6×x=20,
解得x=2,
∴EF=2.
故答案为:2
点评 本题主要考查了三角形的角平分线、中线以及三角形的面积的计算,解决问题的关键是根据△ABD的面积=20,列出方程求解.解题时注意方程思想的运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.绝对值小于3的所有整数的和是( )
| A. | 3 | B. | 0 | C. | 6 | D. | -6 |
 如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=40°,则∠ADC=140°.
如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=40°,则∠ADC=140°.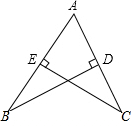 如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.
如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.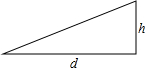 “欲穷千里目,更上一层楼”,经测定,站在距离水平地面h米高的地方看到的水平距离是d米,且h,d之间近似地符合公式d=8$\sqrt{\frac{h}{5}}$,如图所示.登山爱好者小明从n米高的山腰登上2n米高的山顶时,在山顶能看到的水平距离是在山腰能看到的水平距离的多少倍?
“欲穷千里目,更上一层楼”,经测定,站在距离水平地面h米高的地方看到的水平距离是d米,且h,d之间近似地符合公式d=8$\sqrt{\frac{h}{5}}$,如图所示.登山爱好者小明从n米高的山腰登上2n米高的山顶时,在山顶能看到的水平距离是在山腰能看到的水平距离的多少倍?