题目内容
18.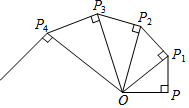 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2017=$\sqrt{2018}$.
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2017=$\sqrt{2018}$.
分析 首先根据勾股定理求出OP4,再由OP1,OP2,OP3的长度找到规律进而求出OP2017的长.
解答 解:由勾股定理得:
OP1=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$;
得OP2=$\sqrt{3}$;
得OP3=2;
OP4=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$;
依此类推可得OPn=$\sqrt{n+1}$,
∴OP2017=$\sqrt{2017+1}$=$\sqrt{2018}$,
故答案为:$\sqrt{2018}$.
点评 本题考查了勾股定理的运用,解题的关键是由已知数据找到规律.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
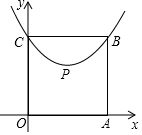 【定义表述】我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”,例如点P(2,4)的特征线有:x=2,y=4,y=x+2,y=-x+6
【定义表述】我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”,例如点P(2,4)的特征线有:x=2,y=4,y=x+2,y=-x+6