题目内容
证明：如果圆的两条切线互相平行，则连接两个切点的线段是圆的直径．
考点：切线的性质
专题：证明题
分析：先写出已知、求证，画出几何图，再进行证明，连结OE、OF，如图，根据切线的性质得OE⊥AB，OF⊥CD，而AB∥CD，根据平行线的性质得OE⊥CD，根据过一点有且只有一条直线与已知直线垂直得到点E、O、F共线，则EF为⊙O的直径．
解答：已知：AB和CD是⊙O的两条平行切线，切点分别为E、F，如图，
求证：EF为⊙O的直径．
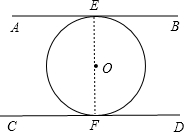证明：连结OE、OF，如图，
∵AB和CD是⊙O的切线，
∴OE⊥AB，OF⊥CD，
∵AB∥CD，
∴OE⊥CD，
∴点E、O、F共线，
∴EF为⊙O的直径．
求证：EF为⊙O的直径．
证明：连结OE、OF，如图，∵AB和CD是⊙O的切线，
∴OE⊥AB，OF⊥CD，
∵AB∥CD，
∴OE⊥CD，
∴点E、O、F共线，
∴EF为⊙O的直径．
点评：本题考查了圆的切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
练习册系列答案
相关题目
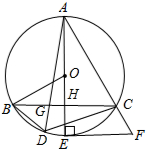如图，AE为⊙O的直径，EF为⊙O的切线，E为切点，连接AF交⊙O于点C，CB∥EF交AE于H交⊙O于B，D为BC弧上一点，连接AD交BC于G．
在△ABC中，AB=AC，点D在BA延长线上，点E在BC上，DC=DE，DE与AC相交于点F，且DF=FE，求证：BE=EC．
小刚和小强玩飞行棋游戏，想要起飞必须投掷一枚骰子，并且得到6，可以起飞之后同时掷两枚骰子，点数之和即为飞行步数．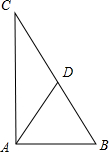
如图，直角△ABC中，∠BAC=90°，D是BC边上的中点，已知sin∠C=