题目内容
已知二次函数y=ax2+bx+c,且ac<0,则它的图象经过( )
| A、一、二、三象限 |
| B、二、三、四象限 |
| C、一、三、四象限 |
| D、一、二、三、四象限 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由ac<0,可判断b2-4ac>0,方程ax2+bx+c=0的有两个异号根,根据抛物线与x轴的交点问题得到抛物线与x轴有两个交点分别在y轴的两侧,然后分类讨论:当a>0时,c<0或
当a<0时,c>0时,根据二次函数图象与系数的关系易得抛物线经过第一、二、三、四象限.
当a<0时,c>0时,根据二次函数图象与系数的关系易得抛物线经过第一、二、三、四象限.
解答:解:∵ac<0,
∴△=b2-4ac>0,方程ax2+bx+c=0的有两个异号根,
∴抛物线与x轴有两个交点,两交点分别在y轴的两侧,
当a>0时,c<0,抛物线经过第一、二、三、四象限;
当a<0时,c>0,抛物线经过第一、二、三、四象限,
综上所述,抛物线经过第一、二、三、四象限.
故选D.
∴△=b2-4ac>0,方程ax2+bx+c=0的有两个异号根,
∴抛物线与x轴有两个交点,两交点分别在y轴的两侧,
当a>0时,c<0,抛物线经过第一、二、三、四象限;
当a<0时,c>0,抛物线经过第一、二、三、四象限,
综上所述,抛物线经过第一、二、三、四象限.
故选D.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中,不是中心对称是( )
A、 |
B、 |
C、 |
D、 |
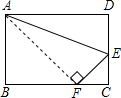 如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=
如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=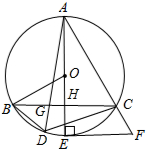 如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G.
如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G. 小刚和小强玩飞行棋游戏,想要起飞必须投掷一枚骰子,并且得到6,可以起飞之后同时掷两枚骰子,点数之和即为飞行步数.
小刚和小强玩飞行棋游戏,想要起飞必须投掷一枚骰子,并且得到6,可以起飞之后同时掷两枚骰子,点数之和即为飞行步数.