题目内容
10．已知二次函数y=ax2+bx+c的x、y的部分对应值如下表：| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
①a＞0；②抛物线的对称轴是直线x=$\frac{3}{2}$；③不等式ax2+bx+c-1＜0的解集是0＜x＜3；④1是方程ax2+（b+1）x+c=0的根．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据表格确定二次函数图象的开口方向以及对称轴，结合表格数据即可对各个选项进行判断．
解答 解：由表格可知：当x越来越大，y先减小后增大，即二次函数图象开口向上，故①正确；
由表格可知：当x=1，y=-1，x=2，y=-1，即抛物线的对称轴为x=$\frac{3}{2}$，故②正确；
不等式ax2+bx+c-1＜0，即ax2+bx+c＜1，根据表格数据可知当1＜x＜3时不等式ax2+bx+c-1＜0，故③正确；
当x=1时，y=a+b+c=-1，故④正确；
正确的选项有4个．
故选D．
点评 本题主要考查了二次函数的性质的知识，解答本题的关键是根据表格发现二次函数图象的对称轴以及开口方向，此题难度不大．
练习册系列答案
名校课堂系列答案
相关题目
17．下列是某校教学活动小组学生的年龄情况：13，15，15，16，13，15，14，15（单位：岁）．这组数据的中位数和极差分别是（ ）
| A． | 15，3 | B． | 14，15 | C． | 16，16 | D． | 14，3 |
18．
发现结论：
（1）n条直线两两相交，最多有$\frac{n（n-1）}{2}$个交点．
（2）由于对顶角是两条直线相交而构成的，每个交点处有两组对顶角，因此可知，对顶角的组数为交点个数的2倍，结合（1），（2）发现结论3：n条直线相交于一点共有n（n-1）组对顶角．
| 直线条数 | 图形 | 最多交点个数 |
| 1 |  | 1 |
| 2 |  | 3=1+2 |
| 3 |  | 6=1+2+3 |
| 4 |  | 10=1+2+3+4 |
（1）n条直线两两相交，最多有$\frac{n（n-1）}{2}$个交点．
（2）由于对顶角是两条直线相交而构成的，每个交点处有两组对顶角，因此可知，对顶角的组数为交点个数的2倍，结合（1），（2）发现结论3：n条直线相交于一点共有n（n-1）组对顶角．
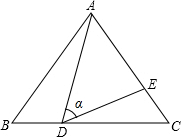如图，在△ABC中，AB=AC=10，点D是边BC上一动点 （不与B，C重合），∠ADE=∠B=α，DE交AC于点E，且$cosa=\frac{4}{5}$．下列结论：
15．方程$\frac{x}{5-x}$-$\frac{2}{3}$=0的解是（ ）
| A． | x=3 | B． | x=-2 | C． | x=2 | D． | x=5 |
