题目内容
20.按要求做题:(1)解方程:3x2+x=3x+1
(2)计算:-22+8÷(-2)3-2×($\frac{1}{8}$$-\frac{1}{2}$)
分析 (1)先变形为x(3x+1)-(3x+1)=0,然后利用因式分解法解方程;
(2)先进行乘方运算,再计算括号内的减法运算,然后进行乘除运算,最后进行加减运算.
解答 解:(1)x(3x+1)-(3x+1)=0,
(3x+1)(x-1)=0,
所以x1=-$\frac{1}{3}$,x2=1;
(2)原式=-4+8÷(-8)-2×(-$\frac{3}{8}$)
=-4-1+$\frac{3}{4}$
=-$\frac{17}{4}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了实数的运算.

练习册系列答案
相关题目
10.在下列各数中是无理数的有( )
$-\sqrt{(-5)^{2}}$、$\sqrt{36}$、$\frac{1}{7}$、0、-π、$\root{3}{11}$、3.1415、$\sqrt{\frac{1}{5}}$、2.010101…(相邻两个1之间有1个0).
$-\sqrt{(-5)^{2}}$、$\sqrt{36}$、$\frac{1}{7}$、0、-π、$\root{3}{11}$、3.1415、$\sqrt{\frac{1}{5}}$、2.010101…(相邻两个1之间有1个0).
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11. 已知a,b,c是三个有理数,它们在数轴上的位置如图所示,则化简|a-b|+|c-a|-|b+c|+(c-a)的结果是( )
已知a,b,c是三个有理数,它们在数轴上的位置如图所示,则化简|a-b|+|c-a|-|b+c|+(c-a)的结果是( )
 已知a,b,c是三个有理数,它们在数轴上的位置如图所示,则化简|a-b|+|c-a|-|b+c|+(c-a)的结果是( )
已知a,b,c是三个有理数,它们在数轴上的位置如图所示,则化简|a-b|+|c-a|-|b+c|+(c-a)的结果是( )| A. | 3a-c | B. | -2a+c | C. | a+c | D. | -2b-c |
 有理数a,b,c在数轴上的位置如图所示,试化简|a-b|-|c+a|+|c-b|-|b|
有理数a,b,c在数轴上的位置如图所示,试化简|a-b|-|c+a|+|c-b|-|b|
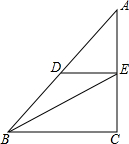 完成求解过程,并写出横线里的理由:
完成求解过程,并写出横线里的理由: 如图,在△ABC中,AD是角平分线,AE是高,已知∠B=50°,∠C=60°,求∠EAD的度数.
如图,在△ABC中,AD是角平分线,AE是高,已知∠B=50°,∠C=60°,求∠EAD的度数.