题目内容
15.阅读下列材料,并解答问题:材料:将分式$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为-x2+1,可设-x4-x2+3=(-x2+1)(x2+a)+b
则-x4-x2+3=(-x2+1)(x2+a)+b=-x4-(a-1)x2+(a+b)
∵对应任意x,上述等式均成立,∴$\left\{\begin{array}{l}{a-1=1}\\{a+b=3}\end{array}\right.$,∴a=2,b=1
∴$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$=$\frac{(-{x}^{2}+1)({x}^{2}+2)+1}{-{x}^{2}+1}$=$\frac{(-{x}^{2}+1)({x}^{2}+2)}{-{x}^{2}+1}$+$\frac{1}{-{x}^{2}+1}$=x2+2+$\frac{1}{-{x}^{2}+1}$
这样,分式$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$被拆分成了一个整式x2+2与一个分式$\frac{1}{-{x}^{2}+1}$的和.
解答:
(1)将分式$\frac{-{x}^{4}-8{x}^{2}+10}{-{x}^{2}+1}$拆分成一个整式与一个分式(分子为整数)的和的形式;
(2)试说明$\frac{-{x}^{4}-8{x}^{2}+10}{-{x}^{2}+1}$的最小值为10.
分析 (1)根据阅读材料中的方法将分式拆分成一个整式与一个分式(分子为整数)的和的形式即可;
(2)原式分子变形后,利用非负数的性质求出最小值即可.
解答 解:(1)设-x4-8x2+10=(-x2+1)(x2+a)+b=-x4-(a-1)x2+(a+b)
∵对应任意x,上述等式均成立,
∴$\left\{\begin{array}{l}{a-1=8}\\{a+b=10}\end{array}\right.$,
∴a=9,b=1.
∴$\frac{-{x}^{4}-8{x}^{2}+10}{-{x}^{2}+1}$=x2+9+$\frac{1}{-{x}^{2}+1}$;
(2)由$\frac{-{x}^{4}-8{x}^{2}+10}{-{x}^{2}+1}$=x2+9+$\frac{1}{-{x}^{2}+1}$=x2-1-$\frac{1}{{x}^{2}-1}$+10知,
令t=x2-1,可知t≥-1,且t≠0;
则原式=t-$\frac{1}{t}+10$,
t>0时,t越大,$\frac{1}{t}$越小,则t-$\frac{1}{t}$+10越大,无最值;
-1≤t<0时,t越大,$\frac{1}{t}$越小,则t-$\frac{1}{t}$+10越大,当t=-1时有最小值,t-$\frac{1}{t}$+10=10,此时x2-1=-1,x=0
因此当x=0时,$\frac{-{x}^{4}-8{x}^{2}+10}{-{x}^{2}+1}$的最小值为10.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
5.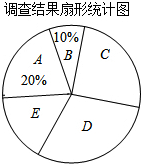 去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
请根据图表中提供的信息解答下列问题:
(1)填空:m=60,n=150,扇形统计图中E组所占百分比为15%;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
 去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | 120 |
| B | 地面灰尘多,空气湿度低 | M |
| C | 汽车尾气排放 | N |
| D | 工厂造成的污染 | 180 |
| E | 其它 | 90 |
(1)填空:m=60,n=150,扇形统计图中E组所占百分比为15%;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
6.-3的相反数是( )
| A. | 3 | B. | -3 | C. | 0 | D. | ±3 |
10.若关于x的方程$\frac{m}{x-4}$-$\frac{1-x}{4-x}$=0有增根,则增根是( )
| A. | -4 | B. | 1 | C. | 4 | D. | -1 |
7. 如图,点A位于点O的( )
如图,点A位于点O的( )
 如图,点A位于点O的( )
如图,点A位于点O的( )| A. | 南偏西25°方向上 | B. | 北偏西65°方向上 | C. | 南偏东65°方向上 | D. | 南偏西65°方向上 |
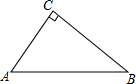 如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8.
如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8.