题目内容
20.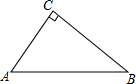 如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8.
如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8.(1)作图:用尺规作AB的垂直平分线,交BC于D,交AB于H.(保留作图痕迹)
(2)在满足(1)的情况下,求BD的长.
分析 (1)垂直平分线的作法为:将圆规的圆心分别处于线段的两端,各做一个圆弧(半径大于线段长的一半),并让其相交,将其交点相连即为该线段垂直平分线;
(2)首先利用勾股定理求得斜边的长,从而求得BH的长,然后利用△BHD∽△BCA求得BD的长即可.
解答 解:(1)如图:
(2)∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵HD垂直平分AB,
∴AH=BH=5,
∵△BHD∽△BCA,
∴$\frac{BD}{BA}=\frac{BH}{BC}$,
即:$\frac{BD}{10}=\frac{5}{8}$,
解得:BD=$\frac{25}{4}$.
点评 本题考查了尺规作图的知识,要牢记:将圆规的圆心分别处于线段的两端,各做一个圆弧(半径大于线段长的一半),并让其相交,将其交点相连即为该线段垂直平分线;

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
10.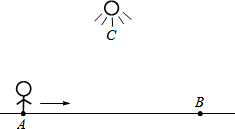 我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
 我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )| A. | y=x? | B. | y=x+3 | C. | y=$\frac{3}{x}$? | D. | y=(x-3)2+3 |
11. 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )
 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )| A. | 38° | B. | 48° | C. | 42° | D. | 100° |
12.分式$\frac{2}{x-3}$有意义,则x的取值范围是( )
| A. | x=3 | B. | x≠3 | C. | x≠-3 | D. | x=-3 |
16.如图,用5个实心圆圈,5个空心圆圈相间组成一个圆环,然后把这样的圆环从左到右按下列规律组成圆环串;相邻两圆环有一公共圆圈,公共圆圈从左到右以实心圆圈和空心圆圈相间排列,
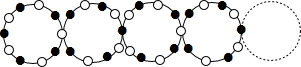
(1)把下列表格补充完整
(2)设圆环串由x个圆环组成,请你直接写出组成这圆环所需实心圆圈和空心圆圈的总个数(用含x的代数式表示);
(3)如果圆环串由这样的圆环20个组成,那么需要多少个空心圆圈?

(1)把下列表格补充完整
| 圆环串中圆环的个数 | 1 | 2 | 3 | 4 | 5 | … |
| 实心圆圈和空心圆圈的总个数 | 10 | 19 | 28 | 37 | 46 | … |
(3)如果圆环串由这样的圆环20个组成,那么需要多少个空心圆圈?
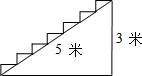 如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯7米.
如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯7米. 如图,等边△ABC内接于⊙O,D是$\widehat{BC}$上任意一点,求证:BD+DC=DA.
如图,等边△ABC内接于⊙O,D是$\widehat{BC}$上任意一点,求证:BD+DC=DA.