题目内容
11.计算:(1)已知△ABC的三边分别是a,b,c,且满足$\sqrt{a-1}+{b^2}-4b+4=0$,求c的取值范围;
(2)${(-1)^{2013}}-|{-3}|+\sqrt{9}×\root{3}{{1-\frac{35}{27}}}-\sqrt{25}×\sqrt{{{(-\frac{2}{5})}^2}}-\root{3}{-0.027}$.
分析 (1)已知等式变形后,利用非负数的性质求出a与b的值,即可确定出第三边c的范围;
(2)原式利用乘方的意义,绝对值的代数意义,平方根及立方根定义计算即可得到结果.
解答 解:(1)∵$\sqrt{a-1}$+(b-2)2=0,
∴a=1,b=2,
则c的范围为1<c<3;
(2)原式=-1-3+3×(-$\frac{2}{3}$)-5×$\frac{2}{5}$+0.3=-1-3-4+0.3=-7.7.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.如图,用5个实心圆圈,5个空心圆圈相间组成一个圆环,然后把这样的圆环从左到右按下列规律组成圆环串;相邻两圆环有一公共圆圈,公共圆圈从左到右以实心圆圈和空心圆圈相间排列,
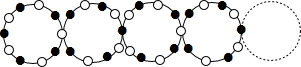
(1)把下列表格补充完整
(2)设圆环串由x个圆环组成,请你直接写出组成这圆环所需实心圆圈和空心圆圈的总个数(用含x的代数式表示);
(3)如果圆环串由这样的圆环20个组成,那么需要多少个空心圆圈?

(1)把下列表格补充完整
| 圆环串中圆环的个数 | 1 | 2 | 3 | 4 | 5 | … |
| 实心圆圈和空心圆圈的总个数 | 10 | 19 | 28 | 37 | 46 | … |
(3)如果圆环串由这样的圆环20个组成,那么需要多少个空心圆圈?
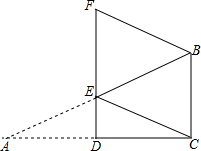 如图,在直角三角形纸片ABC中,∠ACB=90°,把这张纸片沿DE折叠,使点A与C重合,连接CE,过点B作CE的平行线,与DE的延长线交于点F.
如图,在直角三角形纸片ABC中,∠ACB=90°,把这张纸片沿DE折叠,使点A与C重合,连接CE,过点B作CE的平行线,与DE的延长线交于点F.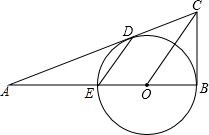 已知:如图,BE是⊙O的直径,BC切⊙O于B,弦ED∥OC,连结CD并延长交BE的延长线于点A.
已知:如图,BE是⊙O的直径,BC切⊙O于B,弦ED∥OC,连结CD并延长交BE的延长线于点A. 如图,在△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点,如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
如图,在△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点,如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动. 已知矩形ABCD的边BC=2AB,E是BC中点,F在DC上,∠FAC=∠EAC.求DF:DC的比值.
已知矩形ABCD的边BC=2AB,E是BC中点,F在DC上,∠FAC=∠EAC.求DF:DC的比值.