题目内容
13.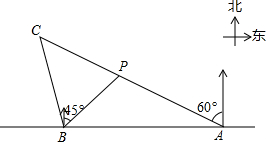 如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.
如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.(1)求小船到海岸线l的距离;
(2)小船从点P沿射线AP方向航行一段时间后,到C处,此时,从点B测得小船在北偏西15°的方向,求此时小船到观测点B的距离.(结果保留根号)
分析 (1)过点P作PD⊥AB于点D,设PD=xkm,先解Rt△PBD,用含x的代数式表示BD,再解Rt△PAD,用含x的代数式表示AD,然后根据BD+AD=AB,列出关于x的方程,解方程即可;
(2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF=$\frac{1}{2}$AB=2km,再解Rt△BCF,得出BC=$\sqrt{2}$BF=2$\sqrt{2}$km.
解答 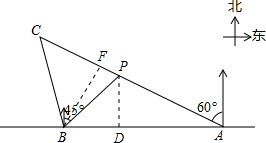 解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,
∴AD=$\sqrt{3}$PD=$\sqrt{3}$xkm.
∵BD+AD=AB,
∴x+$\sqrt{3}$x=4,
x=2($\sqrt{3}$-1),
∴点P到海岸线l的距离为2($\sqrt{3}$-1)km;
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=$\frac{1}{2}$AB=2km.
在△ABC中,∠C=180°-∠BAC-∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=$\sqrt{2}$BF=2$\sqrt{2}$km,
∴点C与点B之间的距离为2$\sqrt{2}$km.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中.通过作辅助线,构造直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.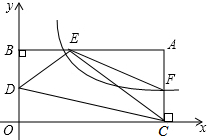 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
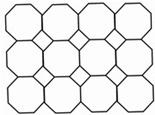 如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要12个小正方形,14小三角形.(不含图案的4个角)
如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要12个小正方形,14小三角形.(不含图案的4个角)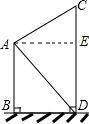 如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70) 如图,小方格都是边长为1的正方形
如图,小方格都是边长为1的正方形