题目内容
17.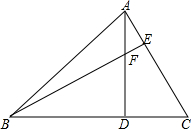 如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE.
如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE.
分析 首先证明△BDF≌△ADC,则∠ADB=∠ADC,∠DBF=∠DAC,据此即可证明∠ADB=∠ADC=90°,然后利用三角形的内角和定理即可证得∠AEF=90°,进而证明垂直.
解答 证明:∵△BDF和△ADC中,
$\left\{\begin{array}{l}{BF=AC}\\{FD=CD}\\{BD=AD}\end{array}\right.$,
∴△BDF≌△ADC,
∴∠ADB=∠ADC,∠DBF=∠DAC,
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴∠DBF+∠BFD=90°,
又∵∠AFE=∠BFD,∠DBF=∠DAC,
∴∠DAC+∠AFE=90°,
∴∠AEF=90°,
∴AC⊥BE.
点评 本题考查了三角形全等的判定与性质以及三角形内角和定理,证明∠ADB=∠ADC=90°是本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
6. 如图,数轴上点A表示一个有理数,则点A与原点的距离为( )
如图,数轴上点A表示一个有理数,则点A与原点的距离为( )
 如图,数轴上点A表示一个有理数,则点A与原点的距离为( )
如图,数轴上点A表示一个有理数,则点A与原点的距离为( )| A. | 1个单位长度 | B. | 2个单位长度 | C. | 3个单位长度 | D. | 4个单位长度 |
7.在y=ax2+bx+c中,如果a>0,b<0,c=0,那么抛物线的顶点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
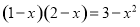 化成一般形式
化成一般形式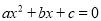 (a≠0),其中a、b、c 的值分别为( )
(a≠0),其中a、b、c 的值分别为( ) 如图,矩形ABCD的对角线相交所成的钝角为120°,短边AB为3cm,则对角线AC长为6cm.
如图,矩形ABCD的对角线相交所成的钝角为120°,短边AB为3cm,则对角线AC长为6cm. 如果二次函数y=ax2+bx+c的图象如图所示,那么反比例函数y=$\frac{b}{x}$的图象的两个分支在第二、四象限.
如果二次函数y=ax2+bx+c的图象如图所示,那么反比例函数y=$\frac{b}{x}$的图象的两个分支在第二、四象限. 如图,在△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
如图,在△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.