题目内容
7.在y=ax2+bx+c中,如果a>0,b<0,c=0,那么抛物线的顶点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由a>0,b<0,可以推出对称轴在y轴的右侧,又c=0,可以得到抛物线与y轴的交点与y轴的交点在原点,所以可以确定顶点位置.
解答  解:∵a>0,
解:∵a>0,
∴抛物线的开口向上,
∵b<0,
∴对称轴为x=-$\frac{b}{2a}$>0,
∴抛物线的对称轴在y轴右侧;
∵c=0,
∴与y轴的交点在原点.
画草图可得:抛物线y=ax2+bx+c的顶点必在第四象限.
故选D.
点评 本题考查了二次函数的图象和二次函数的性质,注意应用数形结合思想,学会画草图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列事件中,是必然事件的是( )
| A. | 任意抛掷一枚硬币,出现正面 | |
| B. | 从2、4、6、8、10这5张卡片中任抽一张是奇数 | |
| C. | 从装有一个红球三个黄球的袋子中任取两球,至少有一个是黄球 | |
| D. | 投掷一枚普通骰子,朝上一面的点数是3 |
12.对于抛物线y=-$\frac{1}{3}$(x-5)2+3,下列说法正确的是( )
| A. | 开口向上,对称轴是直线x=5 | B. | 开口向下,对称轴是直线x=-5 | ||
| C. | 开口向上,对称轴是直线x=-5 | D. | 开口向下,对称轴是直线x=5 |
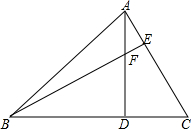 如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE.
如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE.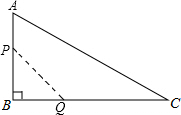 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.