题目内容
9. 如图,在△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
如图,在△ABC中,∠A=40°,∠B=70°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
分析 首先根据三角形的内角和定理求得∠ACB的度数,以及∠BCD的度数,根据角的平分线的定义求得∠BCE的度数,则∠ECD可以求解,然后在△CDF中,利用内角和定理即可求得∠CDF的度数.
解答 解:∵∠A=40°,∠B=70°,
∴∠ACB=180°-∠A-∠B=70°,
∵CE平分∠ACB,
∴∠ACE=$\frac{1}{2}$∠ACB=35°,
∵CD⊥AB于D,
∴∠CDA=90°,
∠ACD=180°-∠A-∠CDA=55°,
∴∠ECD=∠ACD-∠ACE=20°,
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=180°-∠CFD-∠DCE=70°.
点评 本题考查了三角形的内角和等于180°以及角平分线的定义,是基础题,准确识别图形是解题的关键.

练习册系列答案
相关题目
4.下列说法正确的有( )
①等腰三角形是等边三角形;
②三角形按边分可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两边相等;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
①等腰三角形是等边三角形;
②三角形按边分可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两边相等;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
| A. | ①② | B. | ①③④ | C. | ③④ | D. | ①②④ |
14.设a为有理数,则|a|+a的结果( )
| A. | 可能是负数 | B. | 不可能是负数 | ||
| C. | 必定是正数 | D. | 可能是正数,也可能是负数 |
1.下面说法中正确的是( )
| A. | 因为同号相乘得正,所以(-2)×(-3)×(-1)=6 | |
| B. | 任何数和0相乘都等于0 | |
| C. | 若a×b>0,则a>0,b>0 | |
| D. | 以上说法都不正确 |
18.下列事件中,是必然事件的是( )
| A. | 任意抛掷一枚硬币,出现正面 | |
| B. | 从2、4、6、8、10这5张卡片中任抽一张是奇数 | |
| C. | 从装有一个红球三个黄球的袋子中任取两球,至少有一个是黄球 | |
| D. | 投掷一枚普通骰子,朝上一面的点数是3 |
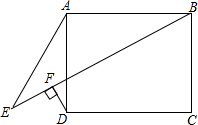 如图,矩形ABCD.AE=CD,DF⊥BE于F.求证:∠E=∠ADF.
如图,矩形ABCD.AE=CD,DF⊥BE于F.求证:∠E=∠ADF.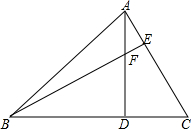 如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE.
如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE.