题目内容
20.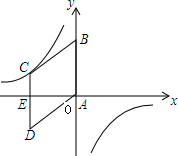 如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点B在y轴的正半轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,点D的坐标为(-4,-3),边CD与x轴交于点E.
如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点B在y轴的正半轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,点D的坐标为(-4,-3),边CD与x轴交于点E.(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当点D落在函数y=$\frac{k}{x}$的图象上时,求菱形ABCD平移的距离.
分析 (1)先根据D点坐标得出OE,DE及OD的长,再由菱形的性质得出CD的长,故可得出C点坐标,代入反比例函数即可得出k的值;
(2)把D点纵坐标代入反比例函数的解析式得出x的值,进而可得出结论.
解答 解:(1)∵点D的坐标为(-4,-3),
∴OE=4,DE=3,OD=5.
∵四边形ABCD是菱形,
∴CD=OD=5,
∴C(-4,2)
∴k=2×(-4)=-8;
(2)∵由(1)知k=-8,
∴反比例函数的解析式为y=-$\frac{8}{x}$.
∵菱形ABCD沿x轴正方向平移,
∴D点纵坐标为-3,
∴-3=$\frac{-8}{x}$,解得x=$\frac{8}{3}$,
∴菱形ABCD平移的距离=$\frac{8}{3}$-(-4)=$\frac{20}{3}$.
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点及菱形的性质等知识,根据题意得出C点坐标是解答此题的关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
11.在解方程$\frac{x-1}{2}$-$\frac{2x+1}{3}$=1时,去分母正确的是( )
| A. | 3(x-1)-2(2x+3)=6 | B. | 3x-3-4x+3=1 | C. | 3(x-1)-2(2x+3)=1 | D. | 3x-3-4x-2=6 |
12.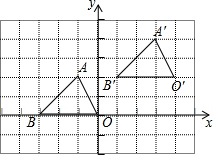 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )| A. | (a,b) | B. | (-a,-b) | C. | (a+2,b+4) | D. | (a+4,b+2) |
9.函数y=$\sqrt{x-2}$+1中,自变量x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
 如图,AC丄BC,AC=9cm,BC=12cm,AB=15cm,点C到直线AB的距离是为$\frac{36}{5}$cm.
如图,AC丄BC,AC=9cm,BC=12cm,AB=15cm,点C到直线AB的距离是为$\frac{36}{5}$cm.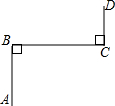 如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.
如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.