题目内容
3.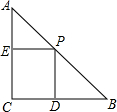 如图.在等腰直角三角形ABC中,斜边AB=$\sqrt{18}$点P在AB上.过P分别作BC,AC的垂线,D,E是垂足.设PD=x,则四边形PDCE的面积S关于x的函数式是S=-x2+3x.
如图.在等腰直角三角形ABC中,斜边AB=$\sqrt{18}$点P在AB上.过P分别作BC,AC的垂线,D,E是垂足.设PD=x,则四边形PDCE的面积S关于x的函数式是S=-x2+3x.
分析 由在等腰直角三角形ABC中,斜边AB=$\sqrt{18}$,根据勾股定理得到AC=BC=3,根据已知条件得到四边形PDCE是矩形,然后由矩形的性质得到CE=PD=x,AE=PE=CD=3-x,即可得到结论.
解答 解:∵在等腰直角三角形ABC中,斜边AB=$\sqrt{18}$,
∴AC=BC=3,
∵PE⊥AC,PD⊥BC,
∴四边形PDCE是矩形,
∴CE=PD=x,
∴AE=PE=CD=3-x,
∴S=CD•PD=(3-x)•x,
即S=-x2+3x.
故答案为:S=-x2+3x.
点评 本题考查了相似三角形的判定和性质,矩形的判定和性质,等腰直角三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
18.已知∠AOB=90°,∠BOC=100°,则射线OC( )
| A. | 在∠AOB内 | B. | 在∠AOB外 | C. | 在∠AOB的内或外 | D. | 有可能与OA重合 |
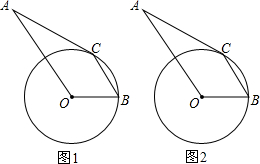 A为⊙O外一点,AC切⊙O于C,BC∥AO.
A为⊙O外一点,AC切⊙O于C,BC∥AO.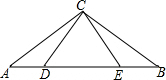 已知:如图,AC=BC,CD=CE,AC⊥EC于C,BC⊥DC于C,求证:AD=BE.
已知:如图,AC=BC,CD=CE,AC⊥EC于C,BC⊥DC于C,求证:AD=BE.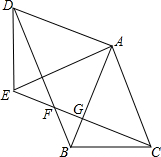 如图,在△ABC中,AB=AC=2,∠BAC=45°,△ABC绕点A顺时针旋转90°后得到△ADE,连接CE、BD、CE交BD于F,交AB于G.
如图,在△ABC中,AB=AC=2,∠BAC=45°,△ABC绕点A顺时针旋转90°后得到△ADE,连接CE、BD、CE交BD于F,交AB于G.