题目内容
15.?ABCD的对角线AC、BD相交于点O,下列条件中,不能判定?ABCD是菱形的是( )| A. | ∠A=∠D | B. | AB=AD | C. | AC⊥BD | D. | CA平分∠BCD |
分析 根据菱形的判定方法一一判断即可解决问题.
解答 解:A、错误.∵∠A=∠D,∠A+∠D=180°,
∴∠A=∠D=90°,
∴四边形ABCD是矩形,不一定是菱形,
故A错误.
B、正确.∵AB=AD,四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
故B正确.
C、正确.∵AC⊥BD,四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
故C正确.
D、正确.∵CA平分∠BCD,AB∥CD
∴∠BAC=∠ACD=∠BCA,
∴BA=BC
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
故D正确.
故选A.
点评 本题考查平行四边形性质,菱形的判定和性质等知识,解题的关键是记住邻边相等的平行四边形是菱形,对角线垂直的平行四边形是菱形,四边相等的四边形是菱形,属于中考常考题型.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
6.在平面直角坐标系中,在第四象限内有一点P,且点P到x轴的距离是4,到y轴的距离是5,则点P的坐标为( )
| A. | (4,-5) | B. | (4,5) | C. | (-5,-4) | D. | (5,-4) |
20.把多项式5x3-5x进行因式分解正确的结果是( )
| A. | 5x3-5x=5(x3-x) | B. | 5x3-5x=5x(x2-1) | ||
| C. | 5x3-5x=5x(x+1)(x-1) | D. | 5x3-5x=5x2(1+$\frac{1}{x}$)(x-1) |
4.下列正多边形的地砖中,不能铺满地面的正多边形是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
5.若用规格相同的正六边形地砖铺地板,则围绕在一个顶点处的地砖的块数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
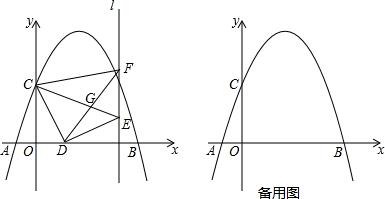
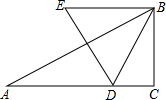 如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.
如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.