题目内容
5．
如图，以原点O为圆心的圆交x轴于A、B两点，交y轴的正半轴与点C，D为第一象限内⊙O上的点，若∠OCD=70°，则∠DAB=25°．
分析 根据圆周角定理求出∠DOB，根据等腰三角形性质求出∠OCD=∠ODC，根据三角形内角和定理求出即可．
解答 
解：连接OD，
∵∠OCD=70°，OD=OC，
∴∠CDO=∠OCD=70°，
∴∠COD=180°-140°=40°，
∴∠DOB=90°-40°=50°，
∴∠DAB=$\frac{1}{2}$∠DOB=25°，
故答案为：25°．
点评 本题考查了圆周角定理，等腰三角形性质，三角形内角和定理的应用，主要考查学生的推理能力，题目比较典型，难度适中．
练习册系列答案
相关题目
15．
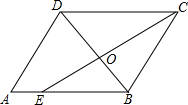如图所示，在?ABCD中，CE是∠DCB的平分线，且交AB于E，DB与CE相交于O，已知AB=6，BC=4，则$\frac{OB}{DB}$等于（ ）
如图所示，在?ABCD中，CE是∠DCB的平分线，且交AB于E，DB与CE相交于O，已知AB=6，BC=4，则$\frac{OB}{DB}$等于（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{7}$ | D． | $\frac{2}{3}$ |
如图AC、BD相交于点O，OA=OD，用“SAS”证△ABO≌△DCO还需条件OB=OC．
如图，已知，在Rt△ABC中，∠C=90°，AB=13，AC=5，⊙O是ABC的内切圆，则这个圆的半径是2．