题目内容
5. 学校要征收一块土地,形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,土地价格为1 000元/m2,请你计算学校征收这块地需要多少钱?
学校要征收一块土地,形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,土地价格为1 000元/m2,请你计算学校征收这块地需要多少钱?
分析 直接利用勾股定理求出AC2的值,再利用勾股定理得出AD的值,进而得出答案.
解答 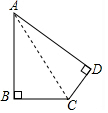 解:连接AC.在△ABC中,∠B=90°,AB=20,BC=15,
解:连接AC.在△ABC中,∠B=90°,AB=20,BC=15,
由勾股定理得:AC2=AB2+BC2=202+152=625.
在△ADC中,∠D=90°,CD=7,
由勾股定理得:AD2=AC2-CD2=625-72=576,AD=24.
所以四边形的面积为:$\frac{1}{2}$AB•BC+$\frac{1}{2}$CD•AD=234(m2).234×1 000=234 000(元).
答:学校征收这块地需要234 000元.
点评 此题主要考查了勾股定理的应用,正确应用构造直角三角形是解题关键.

练习册系列答案
相关题目
20.下列各组线段中,能成比例的是( )
| A. | 3,6,7,9 | B. | 2,5,6,8 | C. | 3,6,9,18 | D. | 1,2,3,4 |
15.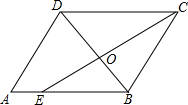 如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )
如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )
 如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )
如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{3}$ |
 如图,正方形OABC顶点AC分别在x轴y轴正半轴上A(m,0)且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解,OB=$\sqrt{2}$OA.
如图,正方形OABC顶点AC分别在x轴y轴正半轴上A(m,0)且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解,OB=$\sqrt{2}$OA.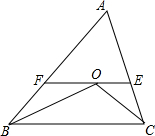 如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.
如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.