Question

8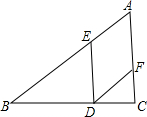．如图，在△ABC中，BC边上有一点D，过D作DE∥AC交AB于E点，过D作DF∥AB交AC于F点．
（1）已知∠EDF=65°，求∠A的度数；
（2）若∠EDB=50°，∠EDF=65°，求∠B、∠C；
（3）结合（1）、（2）猜想：∠A+∠B+∠C等于多少，并加以证明．

Answer 1

分析 （1）根据DE∥AC，DF∥AB，得到四边形AEDF是平行四边形，根据平行四边形的性质即可得到结论；
（2）根据平行线的性质即可得到结论；
（3）根据平行线的性质得到∠BED=∠A，∠BED=∠EDF，∠EDB=∠C，∠FDC=∠B，然后又平角的定义即可得到结论．

解答 解：（1）∵DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∴∠A=∠EDF=65°；

（2）∵DE∥AC，DF∥AB，
∴∠B=∠FDC=180°-∠EDB-∠EDF=65°，∠C=∠EDB=50°；

（3）∠A+∠B+∠C=180°，
∵DE∥AC，DF∥AB，
∴∠BED=∠A，∠BED=∠EDF，∠EDB=∠C，∠FDC=∠B，
∴∠EDF=∠A，
∵∠BDE+∠EDF+∠FDC=180°，
∴∠A+∠B+∠C=180°．

点评 本题考查了三角形的内角和，平行线的性质，平行四边形的判定和性质，平角的定义，熟练掌握各性质定理是解题的关键．