题目内容
2．
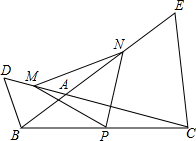如图，已知在△ABC中，延长CA到D，使BA=BD，延长BA到E，使CA=CE，设P、M、N分别是BC、AD、AE的中点．求证：△PMN是等腰三角形．
分析 连接BM、CN，根据等腰三角形三线合一得到∠BMC=90°，根据直角三角形的性质得到MP=$\frac{1}{2}$BC，同理NP=$\frac{1}{2}$BC，得到答案．
解答 证明：
连接BM、CN，
∵BA=BD，DM=MA，
∴BM⊥AD，
∴∠BMC=90°，又BP=PC，
∴MP=$\frac{1}{2}$BC，
同理，NP=$\frac{1}{2}$BC，
∴MP=NP，
∴△PMN是等腰三角形．
点评 本题考查的是直角三角形的性质和等腰三角形的性质，掌握直角三角形斜边上的中线等于斜边的一半、等腰三角形三线合一是解题的关键．
练习册系列答案
相关题目
如图，在等边△ABC中，点D、E分别是AB、BC的中点，AD=6，点P是AD上的一动点，则PE+PB的最小值为6．
有理数a，b，c在数轴上的位置如图所示，化简：$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}$．
如图，OP平分∠BOA，∠BOA=45°，PC∥OA，PD⊥OA．若PC=2$\sqrt{2}$，求PD的长度．