题目内容
17.计算:(1)$\frac{1}{a+1}+\frac{1}{{a}^{2}-1}•\frac{{a}^{2}+2a+1}{a+1}$;
(2)$\frac{{a}^{2}+{b}^{2}}{a+b}•\frac{{a}^{2}-{b}^{2}}{a+b}÷\frac{a-b}{ab({a}^{2}+{b}^{2})}$.
分析 (1)先算乘法,再算加减即可;
(2)从左到右依次计算即可.
解答 解:(1)原式=$\frac{1}{a+1}$+$\frac{1}{(a+1)(a-1)}$•(a+1)
=$\frac{1}{a+1}$+$\frac{1}{a-1}$
=$\frac{a-1+a+1}{(a+1)(a-1)}$
=$\frac{2a}{(a+1)(a-1)}$;
(2)原式=$\frac{{(a}^{2}+{b}^{2})(a-b)}{a+b}$•$\frac{{ab(a}^{2}+{b}^{2})}{a-b}$
=$\frac{{ab(a}^{2}+{b}^{2})^{2}}{a+b}$.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.方程2x-x2$-\frac{2}{x}$=0的实根的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
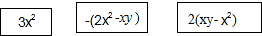
 如图,已知在△ABC中,AB=AC,DE垂直平分AB,垂足为点D,连接BE,BE⊥AC.
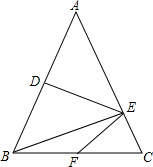
如图,已知在△ABC中,AB=AC,DE垂直平分AB,垂足为点D,连接BE,BE⊥AC.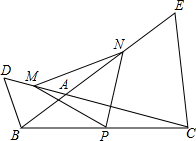 如图,已知在△ABC中,延长CA到D,使BA=BD,延长BA到E,使CA=CE,设P、M、N分别是BC、AD、AE的中点.求证:△PMN是等腰三角形.
如图,已知在△ABC中,延长CA到D,使BA=BD,延长BA到E,使CA=CE,设P、M、N分别是BC、AD、AE的中点.求证:△PMN是等腰三角形. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于F,交BC于E.求证:BE=2CE.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于F,交BC于E.求证:BE=2CE. 如图,图中共有7个三角形,分别是△ABC,△ABE,△BEC,△DBO,△EOC,△BOC,△ADE;∠A的对边是CD,CB,BE;边CD所对的角是∠A、∠ABC.
如图,图中共有7个三角形,分别是△ABC,△ABE,△BEC,△DBO,△EOC,△BOC,△ADE;∠A的对边是CD,CB,BE;边CD所对的角是∠A、∠ABC.