题目内容
12.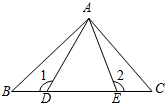 如图,AD=AE,BE=CD,∠1=∠2=130°,∠BAE=60°,则∠C的度数是( )
如图,AD=AE,BE=CD,∠1=∠2=130°,∠BAE=60°,则∠C的度数是( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
分析 运用SAS证明△ABD≌△ACE,得∠B=∠C.根据三角形内角和定理可求∠DAE的度数.则易求∠CAE的度数,进一步即可求得∠C的度数.
解答 解:如图,∵∠1=∠2=110°,
∴∠ADE=∠AED=70°,
∴∠DAE=180°-2×70°=40°.
∵BE=CD,
∴BD=CE.
在△ABD和△ACE中,
$\left\{\begin{array}{l}{BD=CE}\\{∠1=∠2}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE.
∵∠BAE=60°,
∴∠BAD=∠CAE=20°,
∴∠C=180°-∠CAE-∠2=50°.
故选D.
点评 此题考查等腰三角形的判定和性质及三角形内角和定理,证明三角形为等腰三角形是关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
3.下列式子中,正确的是( )
| A. | -4+(-4)=0 | B. | -32=-6 | C. | -3+3=0 | D. | (-1)2=-1 |
4.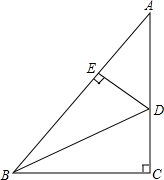 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )
 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=20cm,BC=12cm,△ABC的面积为96cm2,则DE的长是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |