题目内容
4.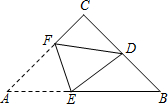 如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为$\frac{3}{5}$.
如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为$\frac{3}{5}$.
分析 先根据翻折变换的性质得到△DEF≌△AEF,再根据等腰三角形的性质及三角形外角的性质可得到∠BED=CDF,设CD=1,CF=x,则CA=CB=2,再根据勾股定理即可求解.
解答 解:∵△DEF是△AEF翻折而成,
∴△DEF≌△AEF,∠A=∠EDF,
∵△ABC是等腰直角三角形,
∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,
∴∠BED=∠CDF,
设CD=1,CF=x,则CA=CB=2,
∴DF=FA=2-x,
∴在Rt△CDF中,由勾股定理得,CF2+CD2=DF2,即x2+1=(2-x)2,
解得x=$\frac{3}{4}$,
∴sin∠BED=sin∠CDF=$\frac{CF}{DF}$=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$
点评 本题考查的是图形翻折变换的性质、等腰直角三角形的性质、勾股定理、三角形外角的性质,涉及面较广,但难易适中.

练习册系列答案
相关题目
15.点A在平面直角坐标系中的第二象限,且A点到x轴的距离为3,到y轴的距离为5,则A的坐标为( )
| A. | (-5,3) | B. | (-3,5) | C. | (5,-3) | D. | (3,-5) |
19.点A在直角坐标系中的坐标是(3,4),则点A到x轴和y轴的距离分别是( )
| A. | 3,4 | B. | 3,4 | C. | 4,3 | D. | 4,3 |
14.下列调查中,适合普查的是( )
| A. | 调查中学生最喜爱的电视节目 | B. | 调查某张试卷上的印刷错误 | ||
| C. | 调查某厂家生产的电池的使用寿命 | D. | 调查中学生上网情况 |