Question

9．如图1，△ABC和△DEF是两块可以完全重合的三角板，∠BAC=∠EDF=90°，∠ABC=∠DEF=30°，在如图1所示的状态下，△DEF固定不动，将△ABC沿直线n向左平移

（1）当△ABC移到图2位置时连接AF，DC，求证：AF=DC；
（2）如图3，在上述平移过程中，当点C与EF的中点重合时，直线n与AD有什么位置关系，请写出证明过程．

Answer 1

分析 （1）先找出相等条件，利用三角形全等的判定定理得出三角形全等，从而对应边相等得出结论．
（2）根据边角关系得出四边形ACDF为菱形，菱形的对角线互相垂直，证出结论．

解答 （1）证明：∵△ABC和△DEF是两块可以完全重合的三角板，
∴AB=DE，BC=EF，
又∵BF=BC-CF，EC=EF-CF，
∴BF=EC，
在△ABF和△DEC中，AB=DE，BF=EC，∠ABC=∠DEF，
∴△ABF≌△DEC（SAS），
∴AF=DC，
证毕．
（2）直线n与AD垂直，
证明：连接AD，如图，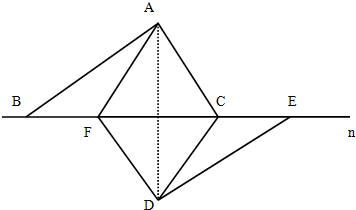
∵△ABC和△DEF是两块可以完全重合的三角板，且∠BAC=∠EDF=90°，∠ABC=∠DEF=30°，
∴∠ACB=∠DFE=60°，AC=DF，
∴AC∥DF，四边形ACDF为平行四边形，
在△DEF中，∠DFE=60°，∠DEF=30°，∠EDF=90°，且点C为线段EF的中点，
∴DC=CF=CE，
在△CDF中，DC=CF，∠DFE=60°，
∴△DCF为等边三角形，DF=DC，
又∵四边形ACDF为平行四边形，
∴四边形ACDF为菱形，
∴AD⊥CF，即AD⊥n，
证毕，
故直线n与AD垂直成立．

点评 本题考查了三角形的判定定理和菱形对角线互相垂直的性质，解题的关键是找对相等的边角．