题目内容
1.我们给出如下定义:两个图形G1和G2,在G1上的任意一点P引出两条垂直的射线与G2相交于点M、N,如果PM=PN,我们就称M、N为点P的垂等点,PM、PN为点P的垂等线段,点P为垂等射点.(1)如图1,在平面直角坐标系xOy中,点P(1,0)为x轴上的垂等射点,过A(0,3)作x轴的平行线l,则直线l上的B(-2,3),C(-1,3),D(3,3),E(4,3)为点P的垂等点的是B(-2,3),E(4,3);
(2)如果一次函数图象过M(0,3),点M为垂等射点P(1,0)的一个垂等点且另一个垂等点N也在此一次函数图象上,在图2中画出示意图并写出一次函数表达式;
(3)如图3,以点O为圆心,1为半径作⊙O,垂等射点P在⊙O上,垂等点在经过(3,0),(0,3)的直线上,如果关于点P的垂等线段始终存在,求垂等线段PM长的取值范围(画出图形直接写出答案即可).
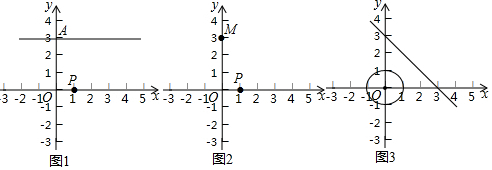
分析 (1)如图1,分别过B,E作BGx轴⊥于G,EH⊥x轴于H,根据等腰直角三角形的判定和性质即可得到结论;
(2)①如图2,当垂等点N直线PM右侧时,根据余角的性质得到∠OMP=∠NPF.根据全等三角形的性质得到PF=OM,OP=FN.求得OF=4,FN=1.得到N(4,1).于是得到结论;②如图3,当垂等点N直线PM左侧时,同理得到结论;
(3)如图4,当点P在第一和第三象限的角平分线上且PM∥OA时,PM取得最小或最大值,延长MP交OB于C,连接OP,根据已知条件得到直线AB的解析式为y=-x+3,根据等腰直角三角形的性质得到OC=PC=$\frac{\sqrt{2}}{2}$,于是得到结论.
解答 解:(1)如图1,分别过B,E作BGx轴⊥于G,EH⊥x轴于H,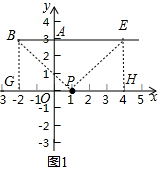
∴BG=EH=3,PG=PH=3,
∴PB=PE=3$\sqrt{2}$,∠BPG=∠EPH=45°,
∴∠BPE=90°,B(-2,3),E(4,3)为点P的垂等点,
故答案为:B(-2,3),E(4,3);
(2)①如图2,当垂等点N直线PM右侧时,
依题意,可知∠MOP=∠MPN=∠NFP=90°,PM=PN,
∵∠OPM+∠OMP=∠OPM+∠NPF=90°,
∴∠OMP=∠NPF.
在△MOP与△PFN中,$\left\{\begin{array}{l}{∠MOP=∠NFP}\\{∠OMP=∠FPN}\\{PM=PN}\end{array}\right.$,
∴△MOP≌△PFN.
∴PF=OM,OP=FN.
∵P(1,0),
∴OF=4,FN=1.
∵点N在第一象限,
∴N(4,1).
∴过点M、N的一次函数表达式为y=-$\frac{1}{2}$x+3;
②如图3,当垂等点N直线PM左侧时,
依题意同理可得N(-2,-1)
∴过点M、N的一次函数表达式为y=2x+3;
(3)如图4,
当点P在第一和第三象限的角平分线上且PM∥OA时,PM取得最小或最大值,
延长MP交OB于C,连接OP,
∵B(3,0),A(0,3),
∴直线AB的解析式为y=-x+3,
∵OP=1,
∴OC=PC=$\frac{\sqrt{2}}{2}$,
∴N的纵坐标为$\frac{\sqrt{2}}{2}$,
∴横坐标为3-$\frac{\sqrt{2}}{2}$,
∴PM=PN=3-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=3-$\sqrt{2}$,同理P′M′=P′M′=3$+\sqrt{2}$,
∴PM长的取值范围:3-$\sqrt{2}$≤PM≤3+$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,待定系数法求函数的解析式,解直角三角形,正确的作出图形是解题的关键.

 名校课堂系列答案
名校课堂系列答案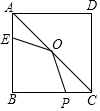 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )| A. | 4+3$\sqrt{2}$ | B. | $\sqrt{29}$+$\sqrt{5}$ | C. | 2+$\sqrt{5}$+3$\sqrt{2}$ | D. | $\sqrt{5}$+$\sqrt{2}$ |
| 汽车行驶时间t(小时) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(升) | 100 | 94 | 88 | 82 | … |
(2)根据上表可知,该车邮箱的大小为100升,每小时耗油6升;
(3)请求出两个变量之间的关系式(用t来表示Q)
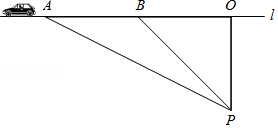 交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73). 如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.