题目内容
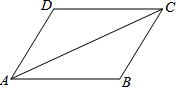 如图,∠D=120°,AB∥DC,且AC平分∠DAB,则∠BAC=
如图,∠D=120°,AB∥DC,且AC平分∠DAB,则∠BAC=考点:平行线的性质
专题:
分析:先根据平行线的性质求出∠DAB的度数,再由角平分线的性质即可得出结论.
解答:解:∵∠D=120°,AB∥DC,
∴∠DAB=180°-120°=60°.
∵AC平分∠DAB,
∴∠BAC=
∠DAB=
×60°=30°.
故答案为:30°.
∴∠DAB=180°-120°=60°.
∵AC平分∠DAB,
∴∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:30°.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
x=1是关于x的一元二次方程x2+mx-5=0的一个根,则此方程的另一个根是( )
| A、5 | B、-5 | C、4 | D、-4 |
下列代数式中,互为同类项的是( )
| A、-2a2b与3ab2 |
| B、18x2y2与9x2+2y2 |
| C、a+b与a-b |
| D、-xy2与y2x |
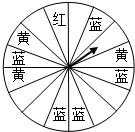 某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.
某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.