题目内容
7．已知关于X的一元二次方程为：x2+2x+2k-4=0．（1）当方程有两实数根时，求k的取值范围；
（3）任取一个k值，求出方程的两个不相等实数根．
分析 （1）根据方程有两实数根可知△≥0，列出关于k的不等式，解之可得；
（2）取k=2，还原方程求解即可．
解答 解：（1）根据题意得：△=22-4（2k-4）≥0，
解得：k≤$\frac{5}{2}$；
（2）取k=2，则方程为x2+2x=0，
即x（x+2）=0，
解得：x=0或x=-2．
点评 本题主要考查根的判别式，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：①当△＞0时，方程有两个不相等的两个实数根；②当△=0时，方程有两个相等的两个实数根；③当△＜0时，方程无实数根．
练习册系列答案
相关题目
15．
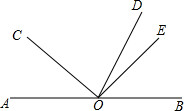如图，点O是直线AB上一点，OD平分∠BOC，∠COE=90°．
（1）若∠AOC=36°，求∠DOE的度数；
（2）若∠AOC=α，则∠DOE=$\frac{1}{2}$α．（用含α的代数式表示）
如图，点O是直线AB上一点，OD平分∠BOC，∠COE=90°．（1）若∠AOC=36°，求∠DOE的度数；
（2）若∠AOC=α，则∠DOE=$\frac{1}{2}$α．（用含α的代数式表示）
如图，在△ABC中，AB=AC，AB的垂直平分线交AB于N，交AC于M．
12．把一条弯曲的河道改成直道，可以缩短航程，其中的道理可以解释为（ ）
| A． | 线段有两个端点 | B． | 两点之间，直线最短 | ||
| C． | 两点之间，线段最短 | D． | 线段可以比较大小 |
已知某市2015年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系如图．