题目内容
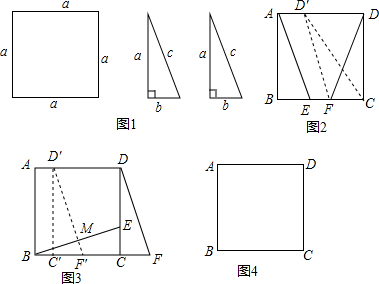
16.问题背景:数学活动课上老师出示问题,如图1,有边长为a的正方形纸片一张,三边长分别为a、b、c的全等直角三角形纸片两张,且b$<\frac{a}{2}$.请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).解决问题:
下面是两个学习小组拼出图案后提出的问题,请你解决他们提出的问题.
(1)“爱心”小组提出的问题是:如图2,将△DFC绕点F逆时针旋转,使点D恰好落在AD边上的点D′处,猜想此时四边形AEFD′是什么特殊四边形,并加以证明;
(2)“希望”小组提出的问题是:如图3,点M为BE中点,将△DCF向左平移至DF恰好过点M时停止,且补充条件a=6,b=2,求△DCF平移的距离.
自主创新:
(3)请你仿照上述小组的同学,在下面图4的空白处用实线画出你拼出的图案,用虚线画出变换图,并在横线处写出你提出的问题.(不必解答)
你提出的问题:当a=6,b=2时,点M,N分别为AD,BC中点,将△MNF沿CB方向移动,使点M落在点A处时,在AB上,AF′交ME于G,求△GEF的面积..
分析 (1)由正方形的性质得结论判断出四边形GFCD为矩形,然后用平行且相等判断出四边形AEFD′是平行四边形;
(2)先判断出△BMF为直角三角形,再根据勾股定理求出BE,判断出△BMF′∽△BCE,用比例式计算即可.
提出的问题:当a=6,b=2时,点M,N分别为AD,BC中点,将△MNF沿CB方向移动,使点M落在点A处时,在AB上,AF′交ME于G,求△GEF的面积,
用平移得特征得EH=F′H=$\frac{1}{2}$EF′=$\frac{1}{2}$,在用三角形的面积公式计算.
解答 证明:(1)作FG⊥AD,
∵四边形ABCD是正方形,
∴∠ADC=∠C=90°,AD∥BC,
∴四边形GFCD是矩形,
∴GD=FC=b,
∴FD=FD′,
∴D′G=DG=b,
∴AD′=AD-2DG=a-2b,
∵BE=FC=b,
∴EF=BC-2FC=a-2b,
∴AD′=EF,
∵AD′∥EF,
∴四边形AEFD′是平行四边形,
(2)由平移知,∠C′D′F′=∠CDF=∠EBC,
∵∠C′D′F′+∠BF′M=90°,
∴∠MBF′+∠BF′M=90°,
∴∠BMF′=90°,
由勾股定理得,BE=$\sqrt{B{C}^{2}+E{C}^{2}}$=2$\sqrt{10}$,
∵点M为BE中点,
∴BM=$\sqrt{10}$,
∵∠BMF′=∠BCE,∠MBF′=∠CBE,
∴△BMF′∽△BCE,
∴$\frac{BM}{BC}=\frac{BF′}{BE}$,
∴$\frac{\sqrt{10}}{6}=\frac{BF′}{2\sqrt{10}}$,
∴BF′=$\frac{10}{3}$,
∵BF=BC+CF=8,
∴F′F=BF-BF′=$\frac{14}{3}$,
∴△DCF平移得距离为$\frac{14}{3}$;
提出的问题:
当a=6,b=2时,点M,N分别为AD,BC中点,将△MNF沿CB方向移动,使点M落在点A处时,在AB上,AF′交ME于G,求△GEF的面积
如图,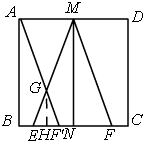
∵MN=BC=b=6,NF=BF′=a=2,
∴FC=BE=F′N=1,
∴EF′=1,
∴EH=F′H=$\frac{1}{2}$EF′=$\frac{1}{2}$,
∵GH∥AB,
∴$\frac{F′H}{BF′}=\frac{GH}{AB}$
∴$\frac{\frac{1}{2}}{2}=\frac{GH}{6}$,
∴GH=$\frac{3}{2}$,
∴S△GEF′=$\frac{1}{2}$×EF′×GH=$\frac{3}{4}$.
点评 此题是四边形综合题,主要考查了正方形的性质,矩形的性质和判定,勾股定理,相似三角形的性质和判定,平移得性质,解本题的关键是判断△BMF是直角三角形.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | 20cm2 | B. | 300cm2 | C. | 400cm2 | D. | 600cm2 |
| A. | $-\frac{1}{3}<-\frac{3}{2}<-0.2<-1$ | B. | $-\frac{1}{3}<-0.2<-1<-\frac{3}{2}$ | C. | $-\frac{3}{2}>-1>-\frac{1}{3}>-0.2$ | D. | $-0.2>-\frac{1}{3}>-1>-\frac{3}{2}$ |
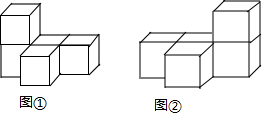
| A. | 主视图 | B. | 俯视图 | ||
| C. | 左视图 | D. | 主视图、俯视图和左视图都不同 |
| A. | 若m>n,则mc>nc | B. | 若m>n,则mc2>nc2 | ||
| C. | 若m>b,b<c,则m>c | D. | 若m+c2>n+c2,则m>n |

 如图,①当AD∥BC时,∠DAC=∠BCA,②当DC∥AB时,∠ADC+∠DAB=180°.
如图,①当AD∥BC时,∠DAC=∠BCA,②当DC∥AB时,∠ADC+∠DAB=180°.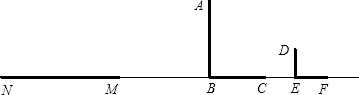
 如图所示,几何体是一个由4个相同的正方体组成的,它的左视图是( )
如图所示,几何体是一个由4个相同的正方体组成的,它的左视图是( )


