题目内容
把二次函数y=-
x2+
x-1化成y=a(x-h)2+k的形式.
(1)指出抛物线的开口方向,对称轴及顶点坐标;
(2)画出函数的图象;
(3)利用图象说明y的值随自变量x值的变化情况.
| 1 |
| 4 |
| 1 |
| 2 |
(1)指出抛物线的开口方向,对称轴及顶点坐标;
(2)画出函数的图象;
(3)利用图象说明y的值随自变量x值的变化情况.
考点:二次函数的三种形式,二次函数的图象,二次函数的性质
专题:
分析:(1)用配方法将y=-
x2+
x-1化成y=a(x-h)2+k的形式,再得出开口方向,对称轴及顶点坐标即可;
(2)再求得抛物线与x轴的交点坐标和y轴的交点坐标,再画图即可;
(3)根据开口方向和对称轴得出y的值随自变量x值的变化情况.
| 1 |
| 4 |
| 1 |
| 2 |
(2)再求得抛物线与x轴的交点坐标和y轴的交点坐标,再画图即可;
(3)根据开口方向和对称轴得出y的值随自变量x值的变化情况.
解答: 解:(1)y=-
解:(1)y=-
x2+
x-1
y=-
(x2-2x)-1,
y=-
(x2-2x+1-1)-1,
y=-
(x-1)2+
-1,
y=-
(x-1)2-
;
∴开口方向向下,对称轴为直线x=1,顶点坐标为(1,-
);
(2)令y=0,得-
(x-1)2-
=0,得(x-1)2=-3,所以方程无解,抛物线与x轴无交点;
令x=0,得y=-1,抛物线与y轴的交点坐标(0,-1);
画图象得:
(3)由图象得出:当x>1时,y随x的增大而减小;当x<1时,y随x的增大而减小.
 解:(1)y=-
解:(1)y=-| 1 |
| 4 |
| 1 |
| 2 |
y=-
| 1 |
| 4 |
y=-
| 1 |
| 4 |
y=-
| 1 |
| 4 |
| 1 |
| 4 |
y=-
| 1 |
| 4 |
| 3 |
| 4 |
∴开口方向向下,对称轴为直线x=1,顶点坐标为(1,-
| 3 |
| 4 |
(2)令y=0,得-
| 1 |
| 4 |
| 3 |
| 4 |
令x=0,得y=-1,抛物线与y轴的交点坐标(0,-1);
画图象得:
(3)由图象得出:当x>1时,y随x的增大而减小;当x<1时,y随x的增大而减小.
点评:本题考查了二次函数的三种形式、二次函数的图象以及二次函数的性质,注意画图的五步:开口方向,对称轴及顶点坐标,与x轴的交点坐标和y轴的交点坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一次函数y=2x-4的图象一定经过点( )
| A、(1,2) |
| B、(1,-2) |
| C、(2,4) |
| D、(2,-4) |
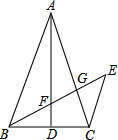 如图,已知△ABC中,AB=AC,D为BC的中点,CE∥AB,BE交AD、AC于E、G,求证:BF2=FG•FE.
如图,已知△ABC中,AB=AC,D为BC的中点,CE∥AB,BE交AD、AC于E、G,求证:BF2=FG•FE.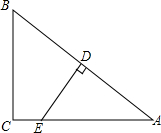 如图,△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB交AC于E,BC=6cm,sin∠A=
如图,△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB交AC于E,BC=6cm,sin∠A=