题目内容
16．化简：（$\sqrt{2}+\sqrt{3}+\sqrt{5}$）2+（$\sqrt{2}+\sqrt{3}-\sqrt{5}$）2+（$\sqrt{2}-\sqrt{3}+\sqrt{5}$）2+（-$\sqrt{2}+\sqrt{3}+\sqrt{5}$）2．分析 利用完全平方公式展开，然后合并即可．
解答 解：原式=（$\sqrt{2}$+$\sqrt{3}$）2+2（$\sqrt{2}$+$\sqrt{3}$）×$\sqrt{5}$+5+（$\sqrt{2}$+$\sqrt{3}$）2-2（$\sqrt{2}$+$\sqrt{3}$）×$\sqrt{5}$+5+[$\sqrt{5}$+（$\sqrt{2}$-$\sqrt{3}$）]2+[$\sqrt{5}$-（$\sqrt{2}$-$\sqrt{3}$）]2
=2（5+2$\sqrt{6}$）+10+5+2（$\sqrt{2}$-$\sqrt{3}$）×$\sqrt{5}$+（$\sqrt{2}$-$\sqrt{3}$）2+5-2（$\sqrt{2}$-$\sqrt{3}$）×$\sqrt{5}$+（$\sqrt{2}$-$\sqrt{3}$）2
=2（5+2$\sqrt{6}$）+10+10+2（5-2$\sqrt{6}$）
=10+10+10+10
=40．
点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．
练习册系列答案
相关题目
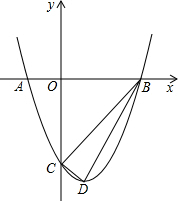如图，在平面直角坐标系中，抛物线y=x2-2x-3与x轴交于A．B两点，点A在x轴负半轴，点B在x轴正半轴，与y轴交于点C，顶点为D．