题目内容
4. 如图,已知A、B、C在⊙O上,∠A=∠B=19°,则∠AOB的度数是( )
如图,已知A、B、C在⊙O上,∠A=∠B=19°,则∠AOB的度数是( )| A. | 68° | B. | 66° | C. | 78° | D. | 76° |
分析 利用圆周角定理可知∠AOB=2∠C,根据三角形的内角和定理得出$\frac{1}{2}$∠AOB=∠OAC+∠OBC=2×19=38°,从而求得∠AOB=76°.
解答  解:连接AB,如图,
解:连接AB,如图,
∵∠OAB+∠OBA+∠AOB=180°,∠OAB+∠OBA+∠OAC+∠OBC+∠C=180°
∴∠AOB=∠OAC+∠OBC+∠C,
∴∠C=$\frac{1}{2}$∠AOB,
∴$\frac{1}{2}$∠AOB=∠OAC+∠OBC=2×19=38°,
∴∠AOB=76°.
故选D.
点评 本题主要考查圆周角定理,掌握在同圆或等圆中同弧所对的圆周角是圆心角的一半是解题的关键.

练习册系列答案
相关题目
12.-($\frac{1}{2}$)2的倒数是( )
| A. | -4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | 4 |
19.x取下列各数中的哪个数时,二次根式$\sqrt{x-1}$没有意义( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | 0 |
16.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | $\sqrt{9}$=3 | D. | 2+$\sqrt{5}$=2$\sqrt{5}$ |
 如图,Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D,E,则圆O的半径为2cm.
如图,Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D,E,则圆O的半径为2cm.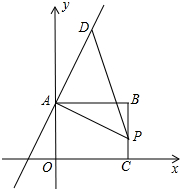 如图,矩形ABC0位于直角坐标平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,6),线段BC上有一动点P,已知点D在第一象限.
如图,矩形ABC0位于直角坐标平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,6),线段BC上有一动点P,已知点D在第一象限.