题目内容
18．
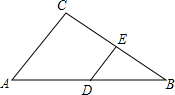如图，在Rt△ABC中，∠C=90°，AB=10，BC=8，DE是△ABC的中位线，则DE=3．
分析 利用勾股定理列式求出AC，再根据三角形的中位线平行于第三边并且等于第三边的一半求解．
解答 解：∵∠C=90°，AB=10，BC=8，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∵DE是△ABC的中位线，
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3．
故答案为：3．
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，勾股定理，熟记定理是解题的关键．
练习册系列答案
相关题目
8．
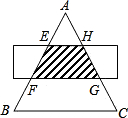如图，△ABC是边长为12cm的等边三角形，被一平行于BC的矩形所截，AB被截成三等分，则图中阴影部分的面积为（ ）
如图，△ABC是边长为12cm的等边三角形，被一平行于BC的矩形所截，AB被截成三等分，则图中阴影部分的面积为（ ）| A． | 16cm2 | B． | $8\sqrt{3}$cm2 | C． | $16\sqrt{3}$cm2 | D． | $12\sqrt{3}$cm2 |
9．画出圆柱从正面，左面，上面看到的形状图
| 图形 | 从正面看 | 从左面看 | 从上面看 |
 |
13．下列因式分解正确的是（ ）
| A． | -a+a3=-a（1+a2） | B． | 2a-4b+2=2（a-2b） | C． | a2-2a+1=（a-1）2 | D． | a2-4=（a-2）2 |
3．完成下列表格，并回答问题：
（1）
由表可知方程2x2-1=0的解在0与1之间．
（2）
由表可知方程2x2-1=0的解在0.7与0.8之间．
…
以此类推，求出方程2x2-1=0的近似解．（精确到0.01）
（1）
| x | 0 | 1 | 2 |
| 2x2-1 | -1 | 1 | 7 |
（2）
| x | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 2x2-1 | -0.5 | -0.28 | -0.2 | 0.28 | 0.62 |
…
以此类推，求出方程2x2-1=0的近似解．（精确到0.01）
10．
如图，为估计池塘两岸A、B间的距离，杨阳在池塘一侧选取了一点P，测得PA=16cm，PB=12m，那么A、B间的距离不可能是（ ）
如图，为估计池塘两岸A、B间的距离，杨阳在池塘一侧选取了一点P，测得PA=16cm，PB=12m，那么A、B间的距离不可能是（ ）| A． | 10m | B． | 15m | C． | 20m | D． | 29m |
已知a，b两数在数轴上的位置如图，化简式子：$\frac{|a|}{-a}$+$\frac{|b|}{b}$．