题目内容
8.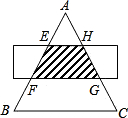 如图,△ABC是边长为12cm的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为( )
如图,△ABC是边长为12cm的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为( )| A. | 16cm2 | B. | $8\sqrt{3}$cm2 | C. | $16\sqrt{3}$cm2 | D. | $12\sqrt{3}$cm2 |
分析 根据题意,易证△AEH∽△AFG∽△ABC,利用相似比,可求出S△AEH、S△AFG面积比,再求出S△ABC,即可得到结果.
解答 解:∵AB被截成三等分,
∴△AEH∽△AFG∽△ABC,
∴$\frac{AE}{AF}$=$\frac{1}{2}$,$\frac{AE}{AB}$=$\frac{1}{3}$,
∴S△AFG:S△ABC=4:9,
S△AEH:S△ABC=1:9,
∴S阴影部分的面积=$\frac{4}{9}$S△ABC-$\frac{1}{9}$S△ABC=$\frac{1}{3}$S△ABC,
∵S△ABC=$\frac{1}{2}$×12×6$\sqrt{3}$=36$\sqrt{3}$,
∴S阴影部分的面积=12$\sqrt{3}$.
故选D.
点评 本题主要考查了利用三等分点求得各相似三角形的相似比,从而求出面积比计算阴影部分的面积,难度适中.

练习册系列答案
相关题目
19.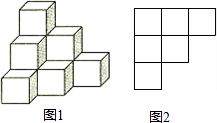 下面说法错误的是( )
下面说法错误的是( )
 下面说法错误的是( )
下面说法错误的是( )| A. | 一个平面截一个球,得到的截面一定是圆 | |
| B. | 一个平面截一个正方体,得到的截面可以是五边形 | |
| C. | 图2是几何体图1的左视图 | |
| D. | 棱柱的截面不可能是圆 |
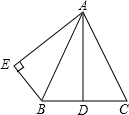 如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.那么AD与AE有什么关系?请说明理由.
如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.那么AD与AE有什么关系?请说明理由.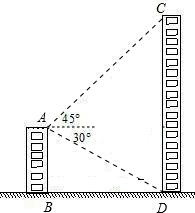 如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).
如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).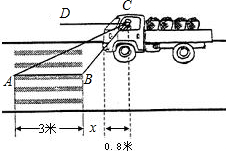 如图,一位驾驶员看到前方斑马线上有行人横穿马路,采取紧急刹车,汽车滑行12米距离后停下,
如图,一位驾驶员看到前方斑马线上有行人横穿马路,采取紧急刹车,汽车滑行12米距离后停下,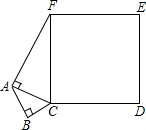 如图,BC=3,AB=4,AF=12,∠FAC和∠ABC都为直角,求正方形FCDE的面积.
如图,BC=3,AB=4,AF=12,∠FAC和∠ABC都为直角,求正方形FCDE的面积.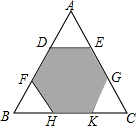 如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小三角形这边长是多少.
如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小三角形这边长是多少.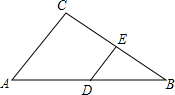 如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,DE是△ABC的中位线,则DE=3.
如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,DE是△ABC的中位线,则DE=3.