题目内容
20.数学综合与实践活动中,某小组测量公园里广场附近古塔的高度.如图,他们先在点D用高1.5米的测角仪DA测得塔顶M的仰角为30°,然后沿DF方向前行40m到达点E处,在E处测得塔顶M的仰角为60°.请根据他们的测量数据求古塔MF的高(结果精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)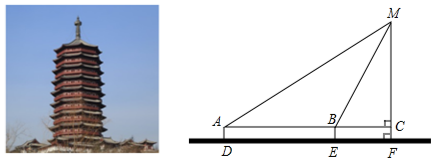
分析 设MC为xm,在Rt△BCM中,得到BC=$\frac{\sqrt{3}}{3}$x,在Rt△AMF中,得到AC=$\sqrt{3}$x,根据AC=AB+BC,列出方程即可解决问题.
解答 解:根据题意,得CF=BE=AD=1.5,AB=DE=40.
设MC为xm,在Rt△MCB中,tan∠1=$\frac{MC}{BC}$,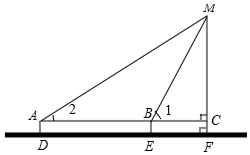
∴BC=$\frac{x}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
同理可得AC=$\sqrt{3}$x,
∴$\sqrt{3}$x=$\frac{\sqrt{3}}{3}$x+40,
解得$x=20\sqrt{3}≈34.64$.…(4分)
∴MF=MC+CF≈34.64+1.5=36.14≈36.1(m)
答:古塔的高约为36.1米.
点评 本题考查解直角三角形,仰角俯角的应用等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
9. 如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是( )
如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是( )
 如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是( )
如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,
以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,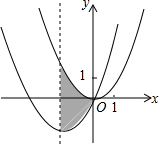 如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.
如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4. 如图,在△ABC中,AC⊥BC,∠B=30°,点E,F是线段AC的三等分点,点P是线段BC上的动点,点Q是线段AC上的动点,若AC=3,则四边形EPQF周长的最小值是8.
如图,在△ABC中,AC⊥BC,∠B=30°,点E,F是线段AC的三等分点,点P是线段BC上的动点,点Q是线段AC上的动点,若AC=3,则四边形EPQF周长的最小值是8.