题目内容
已知:△ABC中,∠ACB=90°,AC=BC,点P是斜边AB上一动点,过点P作CP的垂线,垂直为D,AD的延长线交边CB于点E.
(1)如图1,若∠PCB=22.5°,求证:AC+CE=AB;
(2)如图2,若∠PCB=30°,过点B作CP的垂线,垂足为F,求证:CF=3DE.

(1)如图1,若∠PCB=22.5°,求证:AC+CE=AB;
(2)如图2,若∠PCB=30°,过点B作CP的垂线,垂足为F,求证:CF=3DE.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)连接PE,先利用同角的余角相等得到∠BAE=∠CAE,从而证得△ACD≌△APD,得到AC=AP,再证明△ACE≌△APE,得到∠APE=∠ACE=90,得到∠PEB=∠PBE=45°得到EP=BP=CE,从而得出结论;(2)先利用直角三角形的性质,可证得AD=3DE,再证明△ACD≌△CBF,得到CF=AD,即可得到结论.
解答:解:(1)∵∠PCB=22.5°,∠CAE+∠ACD=90°,∠PCB+∠ACD=90°
∴∠CAE=22.5°
∴∠BAE=45°-22.5°=22.5°,
∴∠BAE=∠CAE
在△ACD与△APD中
∴△ACD≌△APD
∴AC=AP
连接PE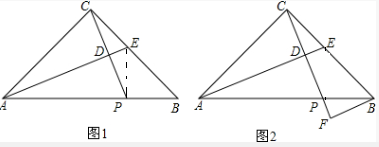
∵AE=AE,∠PAE=∠CAE
在△ACE与△APE中
∴△ACE≌△APE(SAS)
∴∠APE=∠ACE=90°
∴∠BPE=∠APE=90°
∴∠PEB=∠PBE=45°∴EP=BP=CE,
∴AC+CE=AP+PB=AB.
(2)∵∠PCB=30°,∠CAE+∠ACD=90°,
∠PCB+∠ACD=90°
∴∠CAE=∠PCB=30°,
在Rt△CDE中,CE=2ED,在Rt△ACE中,AE=2CE,
∴AE=4DE,AD=3DE
在△ACD和△CFB中,
,
∴△ACD≌△CBF(AAS),
∴CF=AD=3DE
∴∠CAE=22.5°
∴∠BAE=45°-22.5°=22.5°,
∴∠BAE=∠CAE
在△ACD与△APD中
|
∴△ACD≌△APD
∴AC=AP
连接PE

∵AE=AE,∠PAE=∠CAE
在△ACE与△APE中
|
∴△ACE≌△APE(SAS)
∴∠APE=∠ACE=90°
∴∠BPE=∠APE=90°
∴∠PEB=∠PBE=45°∴EP=BP=CE,
∴AC+CE=AP+PB=AB.
(2)∵∠PCB=30°,∠CAE+∠ACD=90°,
∠PCB+∠ACD=90°
∴∠CAE=∠PCB=30°,
在Rt△CDE中,CE=2ED,在Rt△ACE中,AE=2CE,
∴AE=4DE,AD=3DE
在△ACD和△CFB中,
|
∴△ACD≌△CBF(AAS),
∴CF=AD=3DE
点评:本题主要考查全等三角形的判定方法和性质及同角的余角相等,直角三角形的性质等知识,熟练掌握全等三角形的判定方法和相关的性质是解决本题的关键.

练习册系列答案
相关题目