题目内容
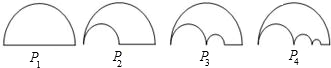
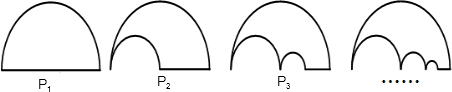
如图,P1是一块半径为1的圆形纸板,把P1剪去一个半径为0.5的圆后得到图形P2,然后依次剪去一个更小的圆(其直径为前一个被剪掉圆的半径)得图形P3,P4,…,Pn,…,记纸板Pn的面积为Sn,当n≥2时,猜想得到Sn-1-Sn是
- A.(
 )2n
)2n - B.π(
 )2n-2
)2n-2 - C.π(
 )2n
)2n - D.π(
 )2n+2
)2n+2
B
分析:根据题意分别用前一个图形的面积减去后一个图形的面积,整理即可发现规律,然后根据规律写出即可.
解答:∵S1=π•12=π,S2=π-π( )2,
)2,
∴S1-S2=π-[π-π( )2]=π(
)2]=π( )2,
)2,
S3=S2-π[( ×
× )]2,
)]2,
∴S2-S3=π[( )2]2,
)2]2,
同理S4=S3-π[( ×
× ×
× )]2,
)]2,
∴S3-S4=π[( )3]2,
)3]2,
…
依此类推:Sn-1-Sn=π[( )n-1]2=π(
)n-1]2=π( )2n-2.
)2n-2.
故选B.
点评:本题是利用圆的面积考查了图形变化规律的问题,求出相邻两个图形的面积的差,并根据数据特点找出变化规律是解题的关键.
分析:根据题意分别用前一个图形的面积减去后一个图形的面积,整理即可发现规律,然后根据规律写出即可.
解答:∵S1=π•12=π,S2=π-π(
 )2,
)2,∴S1-S2=π-[π-π(
 )2]=π(
)2]=π( )2,
)2,S3=S2-π[(
 ×
× )]2,
)]2,∴S2-S3=π[(
 )2]2,
)2]2,同理S4=S3-π[(
 ×
× ×
× )]2,
)]2,∴S3-S4=π[(
 )3]2,
)3]2,…
依此类推:Sn-1-Sn=π[(
 )n-1]2=π(
)n-1]2=π( )2n-2.
)2n-2.故选B.
点评:本题是利用圆的面积考查了图形变化规律的问题,求出相邻两个图形的面积的差,并根据数据特点找出变化规律是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图,P1是一块半径为1的圆形纸板,把P1剪去一个半径为0.5的圆后得到图形P2,然后依次剪去一个更小的圆(其直径为前一个被剪掉圆的半径)得图形P3,P4,…,Pn,…,记纸板Pn的面积为Sn,当n≥2时,猜想得到Sn-1-Sn是( )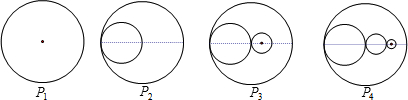

A、(
| ||
B、π(
| ||
C、π(
| ||
D、π(
|