题目内容
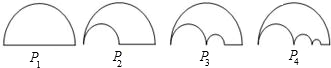
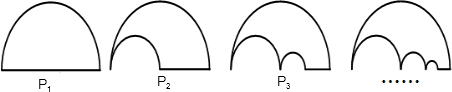
如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为| 1 | 2 |

分析:要求学生首先分析题意,找到规律,并进行推导得出答案.
解答:解:S2=S1-
π(
)2=
-
=
,S3=S2-
π(
)2=
,变形得,S2-S1=-
π(
)2,
S3-S2=-
π(
)2.故可得:Sn-Sn-1=-
(
)n-1.
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 11π |
| 32 |
| 1 |
| 2 |
| 1 |
| 2 |
S3-S2=-
| 1 |
| 2 |
| 1 |
| 4 |
| π |
| 2 |
| 1 |
| 4 |
点评:本题考查学生通过观察、归纳、抽象出数列的规律的能力.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
如图,P1是一块半径为1的圆形纸板,把P1剪去一个半径为0.5的圆后得到图形P2,然后依次剪去一个更小的圆(其直径为前一个被剪掉圆的半径)得图形P3,P4,…,Pn,…,记纸板Pn的面积为Sn,当n≥2时,猜想得到Sn-1-Sn是( )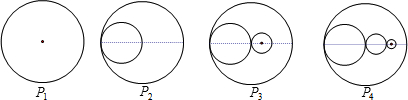

A、(
| ||
B、π(
| ||
C、π(
| ||
D、π(
|