题目内容
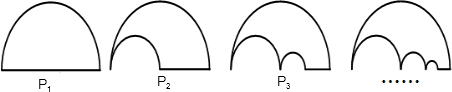
如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为| 1 | 2 |
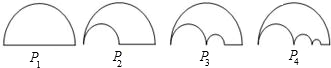
分析:由P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为
的半圆后得到图形P2,得到S1=
π×12=
π,S2=
π-
π×(
)2.同理可得Sn-1=
π-
π×(
)2-
π×[(
)2]2-…-
π×[(
)n-2]2,Sn=
π-
π×(
)2-
π×[(
)2]2-…-
π×[(
)n-2]2-
π×[(
)n-1]2,它们的差即可得到.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:根据题意得,n≥2.
S1=
π×12=
π,
S2=
π-
π×(
)2,
…
Sn-1=
π-
π×(
)2-
π×[(
)2]2-…-
π×[(
)n-2]2,
Sn=
π-
π×(
)2-
π×[(
)2]2-…-
π×[(
)n-2]2-
π×[(
)n-1]2,
∴Sn-1-Sn=
π×(
)2n-2=(
)2n-1π.
故答案为(
)2n-1π.
S1=
| 1 |
| 2 |
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
…
Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn-1-Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为(
| 1 |
| 2 |
点评:本题考查了圆的面积公式:S=πR2.以及规律性题目的解题一般方法:从特殊到一般.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
如图,P1是一块半径为1的圆形纸板,把P1剪去一个半径为0.5的圆后得到图形P2,然后依次剪去一个更小的圆(其直径为前一个被剪掉圆的半径)得图形P3,P4,…,Pn,…,记纸板Pn的面积为Sn,当n≥2时,猜想得到Sn-1-Sn是( )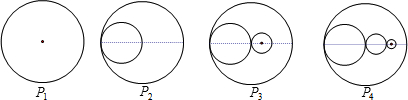

A、(
| ||
B、π(
| ||
C、π(
| ||
D、π(
|