题目内容
12．已知关于x的分式方程$\frac{2x-a}{x+1}$=1的解为正数，则字母a的取值范围是a＞-1．分析 根据解分式方程，可得分式方程的解，根据分式方程的解为正数，可得不等式，根据解不等式，可得答案．
解答 解：方程两边都乘以（x+1），得
2x-a=x+1．
解得x=a+1．
检验：a+1+1≠0，解得a≠-2．
由方程的解为正数，得
a+1＞0，解得a＞-1，
故答案为：a＞-1，
点评 本题考查了分式方程的解，利用分式方程的解是正数得出不等式是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
3．
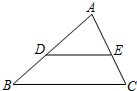如图，△ABC中，点D、E分别为AB、AC上的点，且满足DE∥BC，若AD=3，BD=2，AE=2，则EC的长为（ ）
如图，△ABC中，点D、E分别为AB、AC上的点，且满足DE∥BC，若AD=3，BD=2，AE=2，则EC的长为（ ）| A． | 3 | B． | $\frac{4}{3}$ | C． | $\frac{3}{4}$ | D． | 1 |
如图，一次函数y=k1x-1的图象经过A（0，-1）、B（1，0）两点，与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内的交点为M，若△OBM的面积为1．
如图．E，F在线段BC上，AB=DC，BF=CE，∠B=∠C，求证：AF=DE．