题目内容
3.计算或化简:(1)$\sqrt{18}$+($\sqrt{2}$-1)0$+\sqrt{(1-\sqrt{2})^{2}}$
(2)12$\sqrt{16a}$÷(2$\sqrt{ab}$)×$\frac{1}{6}$$\sqrt{4b}$(a>0,b>0)
分析 (1)根据零指数幂的意义和二次根式的性质计算;
(2)根据二次根式的乘除法则运算.
解答 解:(1)原式=3$\sqrt{2}$+1+$\sqrt{2}$-1
=4$\sqrt{2}$;
(2)原式=12×$\frac{1}{2}$×$\frac{1}{6}$×$\sqrt{16a•\frac{1}{ab}•4b}$
=8.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
18. a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )
 a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )| A. | -a-b | B. | a+b | C. | a-b | D. | b-a |
12.已知x>0,且(x-1)2-324=0,则x+1的值为( )
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
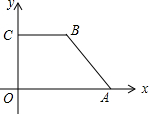 如图,在直角坐标系中,点A、C分别在x轴、y轴上,CB∥OA,CB=8,OC=8,OA=16.
如图,在直角坐标系中,点A、C分别在x轴、y轴上,CB∥OA,CB=8,OC=8,OA=16.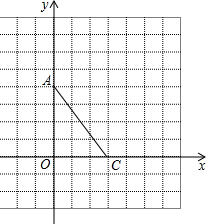 如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.
如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上. 正方形ABCD中,点E为AB的中点,若将△BCE沿CE对折,点B将落在点F处,连接EF并延长交AD、CD的延长线分别于G、H.
正方形ABCD中,点E为AB的中点,若将△BCE沿CE对折,点B将落在点F处,连接EF并延长交AD、CD的延长线分别于G、H.