题目内容
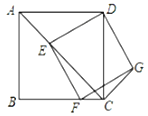
【题目】如图1,![]() ,
,![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,![]() ,
,![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() .
.
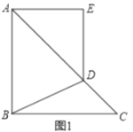
(1)如果![]() ;
;
①求![]() 的值;
的值;
②若![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,求
的两根,求![]() ;
;
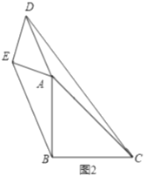
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() .
.
①在![]() 上方,与
上方,与![]() 、
、![]() 、
、![]() 同一平面内找一点
同一平面内找一点![]() ,使四边形
,使四边形![]() 的面积
的面积![]() 四边形
四边形![]() 与四边形
与四边形![]() 的面积
的面积![]() 四边形
四边形![]() 相等,并简要说明寻找点
相等,并简要说明寻找点![]() 的作法;
的作法;
②若![]() 四边形
四边形![]() ,直接写出
,直接写出![]() 的长 .
的长 .
【答案】(1)①![]() ;②
;②![]() ;(2)①说明寻找点F的作法见解析;②
;(2)①说明寻找点F的作法见解析;②![]() .
.
【解析】
(1)①延长![]() 交
交![]() 于
于![]() ,根据勾股定理建立等式即可求出答案;
,根据勾股定理建立等式即可求出答案;
②由根与系数的关系求出a+b及ab,利用①![]() 即可用m分别表示a与b,再整理求出m即可得到答案;
即可用m分别表示a与b,再整理求出m即可得到答案;
(2)①取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长
并延长![]() 至
至![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,![]() 且CF∥DE,
且CF∥DE,![]() 且CE∥DF,根据平行四边形的性质得到
且CE∥DF,根据平行四边形的性质得到![]() ,即可证得结论;
,即可证得结论;
②利用平行四边形的性质根据SAS证明![]() ,得到
,得到![]() 为等腰直角三角形,根据
为等腰直角三角形,根据![]() 四边形
四边形![]() ,求出
,求出![]() 即可求出答案.
即可求出答案.
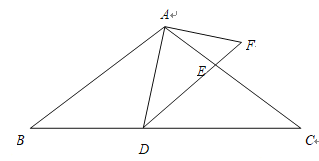
(1)解:①如图1,延长![]() 交
交![]() 于
于![]() ,
,
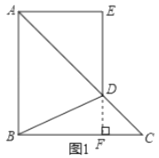
![]() ,
,![]() ,
,
在![]() 中由勾股定理得,
中由勾股定理得,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
又∵![]() ,
,
∴![]() ;
;
②由根与系数的关系![]() ,
,![]() ,
,
由![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,
整理得,![]() ,
,
解得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
当![]() 时,方程为
时,方程为![]() ,这个方程有两个不相等的正根,
,这个方程有两个不相等的正根,
∴![]() 符合题意,
符合题意,
∴![]() ;
;
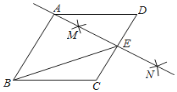
(2)解:①如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长
并延长![]() 至
至![]() ,使OE=OF,连接
,使OE=OF,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,![]() 且CF∥DE,
且CF∥DE,![]() 且CE∥DF,
且CE∥DF,

∴![]()
∴![]() 四边形
四边形![]() 四边形
四边形![]() ;
;
②∵CE∥DF,
∴∠EFC=∠DEF=90°,
∵∠ABC=90°,
∴∠BCF+∠BAF=∠BAF+∠BAE=180°,
∴∠BCF=∠BAE,
∵CF=DE=AE,BC=BA,
∴![]() ,
,
∴EB=FB,∠ABE=∠CBF,
∴∠EBF=90°,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∵![]() 四边形
四边形![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
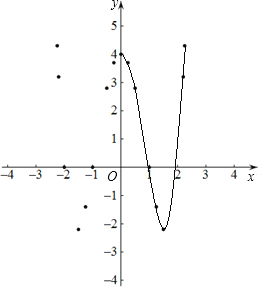
暑假接力赛新疆青少年出版社系列答案【题目】小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
![]() 自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x |
|
|
|
|
|
|
|
|
| 0 |
|
| 1 |
|
| 2 |
|
|
|
y |
|
|
| 0 |
|
| 0 |
|
| 4 |
|
| 0 |
|
| m |
|
|
|
其中![]() _______;
_______;
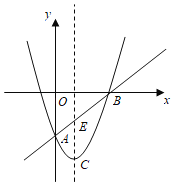
![]() 如图,在平面直角坐标系xOy中,把该函数的图象补充完整;
如图,在平面直角坐标系xOy中,把该函数的图象补充完整;
![]() 观察函数图象,写出一条该函数的性质______;
观察函数图象,写出一条该函数的性质______;
![]() 进一步探究函数图象发现:
进一步探究函数图象发现:
![]() 方程
方程![]() 有______个互不相等的实数根;
有______个互不相等的实数根;
![]() 有两个点
有两个点![]() 和
和![]() 在此函数图象上,当
在此函数图象上,当![]() 时,比较
时,比较![]() 和
和![]() 的大小关系为:
的大小关系为:![]() ______
______![]() 填“
填“![]() ”、“
”、“![]() ”或“
”或“![]() ”
”![]() ;
;
![]() 若关于x的方程
若关于x的方程![]() 有4个互不相等的实数根,则a的取值范围是______.
有4个互不相等的实数根,则a的取值范围是______.