Question

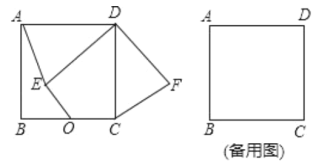
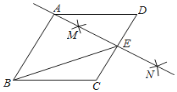
【题目】如图，在菱形中，，按以下步骤作图：①分别以点和点为圆心，为圆心，大于号的长为半径面狐，两弧交于点，：②做直线，且恰好经过点，与交于点，连接，则的值为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

由作法得AE垂直平分CD，则∠AED=90°，CE=DE，于是可判断∠DAE=30°，∠D=60°，作EH⊥BC于H，从而得到∠ECH=60°,利用三角函数可求出EH、CH的值，再利用勾股定理即可求出BE的长.

解：如图所示，作EH⊥BC于H，

由作法得AE垂直平分CD，

∴∠AED=90°，CE=DE＝2，

∵四边形ABCD为菱形，

∴AD=2DE，

∴∠DAE=30°，

∴∠D=60°，

∵AD//BC，

∴∠ECH=∠D=60°,

在Rt△ECH中，

EH=CE·sin60°=,

CH=CE·cos60°=,

∴BH=4+1=5，

在Rt△BEH中，由勾股定理得，

.

故选B.