题目内容
1.解方程组(1)$\left\{\begin{array}{l}x-y=3\\ 3x-8y=14\end{array}\right.$
(2)$\left\{\begin{array}{l}\frac{1}{6}x-\frac{3}{4}y=\frac{5}{4}\\ 4(x-y)-3(2x+y)=1\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-y=3①}\\{3x-8y=14②}\end{array}\right.$,
①×8-②得:5x=10,即x=2,
把x=2代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-9y=15①}\\{-2x-7y=1②}\end{array}\right.$,
①+②得:-16y=16,即y=-1,
把y=-1代入②得:x=3,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
19.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
| A. | 点A在圆上 | B. | 点A在圆内 | C. | 点A在圆外 | D. | 无法确定 |
9.温家宝总理在2012年3月的政府工作报告中指出,2012年,再解决60 000 000农村人口的安全饮水问题.将60 000 000用科学记数法表示应为( )
| A. | 6×106 | B. | 6×107 | C. | 6×108 | D. | 60×106 |
11.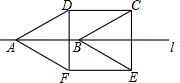 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
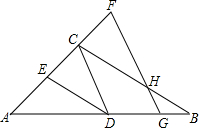 如图,已知∠ADE=∠B,∠EDC+∠CHG=180°,那么∠ECD=∠F吗?为什么?
如图,已知∠ADE=∠B,∠EDC+∠CHG=180°,那么∠ECD=∠F吗?为什么?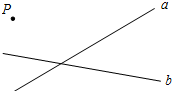 (1)在图中画出表示点P到直线a距离的线段PM;
(1)在图中画出表示点P到直线a距离的线段PM;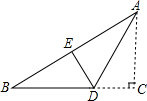 如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处,已知BC=12,∠B=30°,则DE=4.
如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处,已知BC=12,∠B=30°,则DE=4.