题目内容
7.若不等式组$\left\{\begin{array}{l}{2x+3≥0}\\{3x-2<0}\end{array}\right.$的解集是-$\frac{3}{2}$≤x<$\frac{2}{3}$.分析 分别求出各不等式的解集,再求出其公共解集即可.
解答 解:$\left\{\begin{array}{l}2x+3≥0①\\ 3x-2<0②\end{array}\right.$,由①得,x≥-$\frac{3}{2}$,由②得,x<$\frac{2}{3}$,故不等式组得解集为:-$\frac{3}{2}$≤x<$\frac{2}{3}$.
故答案为:-$\frac{3}{2}$≤x<$\frac{2}{3}$.
点评 本题考查的是解一元一次不等式组,熟知同大取大;同小取小;大小小大中间找;大大小小找不到的原则是解答此题的关键.

练习册系列答案
相关题目
15.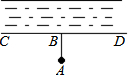 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )| A. | 两点之间线段最短 | B. | 点到直线的距离 | ||
| C. | 两点确定一条直线 | D. | 垂线段最短 |
16.计算:(-1)100+(-1)101的结果是( )
| A. | 1100 | B. | -1 | C. | 0 | D. | -1100 |
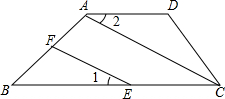 已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠1=∠2.
已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠1=∠2.