题目内容
20.在△ABC中,点D、E分别是边AB、AC上的点,且有$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,BC=18,那么DE的值为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
分析 首先根据题意画出图形,由$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,易证得△ADE∽△ABC,然后由相似三角形的对应边成比例,求得答案.
解答  解:如图,∵$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,
解:如图,∵$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,
∴$\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{1}{3}$,
∵∠A=∠A,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AD}{AB}=\frac{1}{3}$,
∵BC=18,
∴DE=6.
故选B.
点评 此题考查了相似三角形的判定与性质.注意根据题意画出图形,结合图形求解是关键.

练习册系列答案
相关题目
10.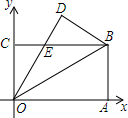 如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )
如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )
 如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )
如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,$\sqrt{3}$) | D. | ($\frac{3}{2}$,$\sqrt{3}$) |
11.70.78亿元用科学记数法表示为( )
| A. | 70.78×108元 | B. | 7.078×108元 | C. | 7.078×109元 | D. | 7.078×1010元 |
8.向东走-800米的意义是( )
| A. | 向东走800米 | B. | 向西走800米 | C. | 向西走-800米 | D. | 以上都不对 |
5.不等式组$\left\{{\begin{array}{l}{x-3≤0}\\{x+1>0}\end{array}}\right.$的解集是( )
| A. | -1<x≤3 | B. | -1<x<3 | C. | x>-1 | D. | x≤3 |
12.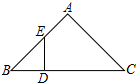 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )| A. | DE=DB | B. | DE=AE | C. | AE=BE | D. | AE=BD |