题目内容
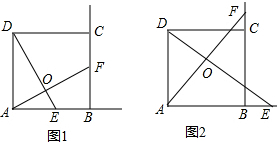
4.已知如图1菱形ABCD,∠ABC=60°,边长为 3,在菱形内作等边三角形△AEF,边长为2$\sqrt{2}$,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
(1)在图2中证明BE=CF;
(2)若∠BAE=45°,求CF的长度;
(3)当CF=$\sqrt{17}$时,直接写出旋转角α的度数.
分析 (1)连接AC,证明△AEB≌△AFC,即可得出结论;
(2)过E点作EM⊥AB于M,则△AEM是等腰直角三角形,得出EM=AM=$\frac{\sqrt{2}}{2}$AE=2,求出BM=AB-AM=1,在Rt△BME中,由勾股定理求出BE,即可得出CF的长;
(3)过E点作EM⊥AB于M,则∠EMB=∠EMA=90°,由(1)得:BE=CF=$\sqrt{17}$,设AM=x,则BM=3-x,由勾股定理得出方程,积解方程求出x=0,得出点M与
A重合,求出∠BAE=90°,即α=90°;同理可得:当CF=$\sqrt{17}$时,α还等于270°即可.
解答  (1)证明:连接AC,如图2所示:
(1)证明:连接AC,如图2所示:
∵四边形ABCD是菱形,
∴AB=BC=3,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵△AEF是等边三角形,
∴AE=AF,∠EAF=60°,
∴∠EAF-∠BAF=∠BAC-∠BAF,
∴∠BAE=∠CAF,
在△AEB和△AFC中,$\left\{\begin{array}{l}{AE=AF}&{\;}\\{∠BAE=∠CAF}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△AEB≌△AFC(SAS),
∴BE=CF;
(2)解:过E点作EM⊥AB于M,如图3所示:
∵∠BAE=45°,则△AEM是等腰直角三角形,
∴EM=AM=$\frac{\sqrt{2}}{2}$AE=$\frac{\sqrt{2}}{2}$×2$\sqrt{2}$=2,
∴BM=AB-AM=3-2=1,
在Rt△BME中,由勾股定理得:BE=$\sqrt{E{M}^{2}+B{M}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
由(1)得:CF=BE=$\sqrt{5}$;
(3)解:过E点作EM⊥AB于M,如图4所示,
则∠EMB=∠EMA=90°,
由(1)得:BE=CF=$\sqrt{17}$,
设AM=x,则BM=3-x,
由勾股定理得:BM2=BE2-BM2,BM2=AE2-AM2,
∴BE2-BM2=AE2-AM2,即($\sqrt{17}$)2-(3-x)2=(2$\sqrt{2}$)2-x2,
解得:x=0,即点M与A重合,
∴∠BAE=90°,即α=90°;
同理可得:当CF=$\sqrt{17}$时,α还等于270°;
综上所述:当CF=$\sqrt{17}$时,旋转角α的度数为90°或270°.
点评 本题是四边形综合题目,考查了菱形的性质、全等三角形的判定与性质、旋转的性质、等边三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识;本题综合性强,有一定难度.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案 如图,两条平行线a、b被直线c所截.若∠1=40°,则∠2=140°.
如图,两条平行线a、b被直线c所截.若∠1=40°,则∠2=140°.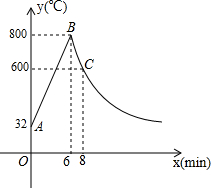 如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
 如图,点A、B、E、D在同一直线上,AC∥DF,AE=BD,AC=DF.
如图,点A、B、E、D在同一直线上,AC∥DF,AE=BD,AC=DF.