题目内容
13.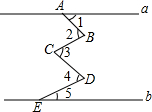 如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.
如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.
分析 作BF∥a,CG∥a,DH∥a,根据两直线平行,内错角相等,找出相等的内错角,分别求和得到答案.
解答  解:∠2+∠4=∠1+∠3+∠5.
解:∠2+∠4=∠1+∠3+∠5.
理由:作BF∥a,CG∥a,DH∥a,
∵a∥b,
∴a∥BF∥CG∥DH∥b,
∴∠1=∠ABF,∠FBC=∠BCG,∠GCD=∠CDH,∠HDE=∠5,
∴∠2+∠4=∠1+∠3+∠5.
点评 本题考查的是平行线的性质.解题的关键是根据平行线的性质证明内错角相等,正确作出辅助线是解答本题的重点.

练习册系列答案
相关题目
18.在Rt△ABC中,∠C=90°,AB=4,D为斜边AB上的一个动点,作DE⊥AC于E,DF⊥BC于F,以EF为直径作一个圆,记圆的周长为l,则下面结论中错误的是( )
| A. | 若∠A=30°,则l的最小值等于$\sqrt{3}$π | B. | 若∠A=45°,则l的最小值等于2π | ||
| C. | 若∠A=60°,则l的最小值等于$\frac{\sqrt{3}}{2}$π | D. | 若EF∥AB,则l等于2π |
3.二次根式$\sqrt{(x+3)^{2}}$中字母x的取值范围是( )
| A. | x≠-3 | B. | x≥-3 | C. | x>-3 | D. | 全体实数 |
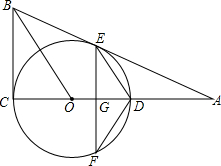 如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.
如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.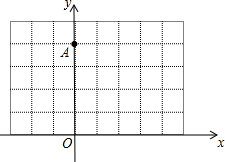 如图,在8×5的小正方形网格中,小正方形的边长为1,点O在格点(网络线的交点)上,且点A的坐标为(0,4).
如图,在8×5的小正方形网格中,小正方形的边长为1,点O在格点(网络线的交点)上,且点A的坐标为(0,4).